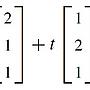作者查詢 / cuylerLin

總覽項目：發文 | 留言 | 暱稱

作者 cuylerLin 在 PTT [ Math ] 看板的留言(推文), 共674則

限定看板：Math

看板排序：

首頁

尾頁

[機統] 一題機率問題

[ Math ]13 留言, 推噓總分: +1

作者: s035280236 - 發表於 2020/11/07 21:01(5年前)

9^F推cuylerLin: 此題概念同於以下文章中我3F的計算，適用性極廣，請11/07 23:26

10^F→cuylerLin: 參考11/07 23:26

11^F→cuylerLin: https://tinyurl.com/y5g4msev11/07 23:26

[微積] 關於拉格朗日函數表示式的疑惑

[ Math ]42 留言, 推噓總分: +6

作者: NINEVEN - 發表於 2020/11/07 22:03(5年前)

8^F推cuylerLin: 推aikotoba大，沒錯 lambda 的正負號其實很重要，個11/07 23:22

9^F→cuylerLin: 經裡會代表某種 marginal utility ，所以不是你喜歡11/07 23:22

10^F→cuylerLin: 怎樣設定就怎樣設定的，當然數學形式上兩者可能沒差11/07 23:22

11^F→cuylerLin: 就是了～11/07 23:22

[機統] 數理統計習題 MLE計算

[ Math ]1 留言, 推噓總分: 0

作者: decalcla - 發表於 2020/11/05 16:30(5年前)

1^F→cuylerLin: 作業題？題目基本上都不難，建議你先去看上課講義吧11/05 16:38

[微積] 請教極值 Lagrange 相關問題

[ Math ]85 留言, 推噓總分: +8

作者: hardandhard - 發表於 2020/11/01 22:08(5年前)

1^F→cuylerLin: 你這不就是一個 w 的二次式而已？要怎樣確認符合範11/01 22:25

2^F→cuylerLin: 圍，兩邊減減看有沒有符合大小關係11/01 22:25

[公告] 關於討論的規定

[ Math ]13 留言, 推噓總分: +2

作者: DLHZ - 發表於 2020/11/01 15:00(5年前)

5^F推cuylerLin: 辛苦版主惹，我才正在想最近幾天爭議十足的推文怎麼11/01 18:40

6^F→cuylerLin: 遲遲沒人檢舉也沒看到水桶或警告文（連稍微緩和局勢11/01 18:43

7^F→cuylerLin: 的一些版友後來也被砲...），就看到這篇了XD11/01 18:43

[微積]拋體運動

[ Math ]1 留言, 推噓總分: +1

作者: rebe212296 - 發表於 2020/11/01 12:13(5年前)

1^F推cuylerLin: t=x/(v0*cos) 代到第二式11/01 13:02

[其他] 離散兩題

[ Math ]21 留言, 推噓總分: +1

作者: LiquidTLO - 發表於 2020/10/29 17:01(5年前)

1^F推cuylerLin: (2) 考慮一開始有沒有選到車子的門10/29 20:22

2^F→cuylerLin: 最後兩個機率加起來你會得 [k(N-1)] /[N(N-j-1)]10/29 20:22

3^F→cuylerLin: 這個機率你想要大於等於 k/N，結果你發現不管怎樣10/29 20:22

4^F→cuylerLin: 這個不等式都成立10/29 20:22

10^F→cuylerLin: 有兩個case要考慮喔，第一次選到門然後換到門，跟第10/29 23:30

11^F→cuylerLin: 一次沒選到門然後換到門，加起來就是我一開始寫的結10/29 23:30

12^F→cuylerLin: 果10/29 23:30

13^F→cuylerLin: 選到車換到車才對，一直打成門XD10/29 23:30

[線代] 矩陣子空間的證明

[ Math ]55 留言, 推噓總分: +3

作者: kbolm - 發表於 2020/10/24 22:47(5年前)

6^F推cuylerLin: 交集空集合顯然；給定任意矩陣A10/24 23:52

7^F→cuylerLin: 定義B(A) (i,j)=B(A) (j,i) =A(i,j) for all i<=j.10/24 23:52

8^F→cuylerLin: A=[A-B(A)] +B(A) 則前項落在W1裡，後項B(A) 落在W210/24 23:52

9^F→cuylerLin: 裡，直和分解成立10/24 23:52

13^F推cuylerLin: 不是，你要證明任意A都可以寫成W1裡面的東西加上W210/24 23:59

14^F→cuylerLin: 裡面的東西，此處的 addition as in matrix additio10/24 23:59

15^F→cuylerLin: n10/24 23:59

16^F→cuylerLin: 也就是你要把A湊出這兩個subspace裡面的元素，至於10/25 00:00

17^F→cuylerLin: 怎麼湊就是經驗了XD10/25 00:00

19^F→cuylerLin: 你可能只是定義不熟而已，可以回去前面1.3章的子空10/25 00:20

20^F→cuylerLin: 間看看～10/25 00:20

29^F→cuylerLin: 原po也沒有毫無章法亂湊吧...我覺得原po只是定義不10/25 00:37

30^F→cuylerLin: 夠熟悉而已10/25 00:37

33^F→cuylerLin: 就是要把任意的矩陣A湊出W1跟W2裡面的元素相加，怎10/25 00:46

34^F→cuylerLin: 麼會扯到毫無章法XD？一定是根據這兩個子空間來湊不10/25 00:46

35^F→cuylerLin: 是嗎XD10/25 00:46

36^F→cuylerLin: 當然可能複雜的題目給經驗多的人做，一下子就湊出來10/25 00:47

37^F→cuylerLin: 可能會被說毫無章法賽到就是了...10/25 00:47

38^F→cuylerLin: 我反而會建議原po其實可以很直覺地馬上把B(A) 寫下10/25 00:49

39^F→cuylerLin: 來10/25 00:49

51^F推cuylerLin: 順帶補充一下，原po也可以做做前一題，收穫也會滿多10/25 01:14

52^F→cuylerLin: 的XD10/25 01:14

[線代] 子空間證明

[ Math ]36 留言, 推噓總分: +4

作者: NTUmaki - 發表於 2020/10/24 10:57(5年前)

21^F推cuylerLin: 題目的意思是這個集合收集的是那些可以用那兩個向量10/24 18:49

22^F→cuylerLin: 組出來的R^3向量，寫法沒有不標準啊，先說這個集合10/24 18:49

23^F→cuylerLin: 是R^3的子集，然後描述裡面成員要長成那兩個向量的10/24 18:49

24^F→cuylerLin: 線性組合，請你證明這個子集是否是子空間，而一個非10/24 18:49

25^F→cuylerLin: 空子集的話就去檢驗VS公設0,1,3,4是否成立，成立即10/24 18:49

26^F→cuylerLin: 為子空間10/24 18:49

27^F→cuylerLin: 有點忘記了，非空可能3跟4可以互推就是了，所以可能10/24 18:51

28^F→cuylerLin: 只要檢驗三個公設10/24 18:51

[機統] 迴歸分析 F檢定

[ Math ]28 留言, 推噓總分: +1

作者: love113w - 發表於 2020/10/20 11:47(5年前)

11^F推cuylerLin: 這兩個F-統計量是一樣的喔，廣泛來說你想把原資料投10/20 18:14

12^F→cuylerLin: 影在兩個models上，一個是null model另一個是altern10/20 18:14

13^F→cuylerLin: ative model，也有人稱restrictive model和unrestri10/20 18:14

14^F→cuylerLin: ctive model，而限制比較多的模型，殘差自然大；分10/20 18:14

15^F→cuylerLin: 母應該沒問題，分子的話由於在空間上他們正交（需要10/20 18:14

16^F→cuylerLin: 線性代數解釋），直接相減就可以找到類比於你一維F10/20 18:14

17^F→cuylerLin: 檢定的情況10/20 18:14

18^F→cuylerLin: 打錯了修正一下。限制比較多的模型，殘差「小」才對10/20 18:15

19^F→cuylerLin: 欸，沒事XD 我原本沒說錯，頭暈惹10/20 18:17

20^F→cuylerLin: 至於證明的話我就不寫了，不是那麼好證，要對大量投10/20 18:19

21^F→cuylerLin: 影來投影去，以及習慣用矩陣來表示回歸結果很熟悉才10/20 18:19

22^F→cuylerLin: 比較好證10/20 18:19

首頁

尾頁