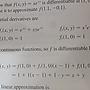作者查詢 / cuylerLin

總覽項目：發文 | 留言 | 暱稱

作者 cuylerLin 在 PTT [ Math ] 看板的留言(推文), 共674則

限定看板：Math

看板排序：

首頁

尾頁

[中學] 猜數字遊戲第一次就猜到3A的機率

[ Math ]18 留言, 推噓總分: +5

作者: hotwei - 發表於 2020/07/23 14:38(5年前)

1^F推cuylerLin: 你的規則好像跟一般的猜數字不一樣，一般猜數字不會07/23 15:22

2^F→cuylerLin: 出現 3A1B，如果依照你的規則的話：07/23 15:22

3^F→cuylerLin: 總樣本空間大小為 C(10,4)*4!07/23 15:22

4^F→cuylerLin: 3A1B 的可能有，先固定 3A: C(4,3)07/23 15:22

5^F→cuylerLin: 剩下的數字從其他 6 個挑: C(6,1)07/23 15:22

6^F→cuylerLin: 所以只有 18 種07/23 15:22

7^F推cuylerLin: 哦，沒事了，你的意思應該是 3A0B07/23 15:26

8^F→cuylerLin: 我以為你是 3A1B XD07/23 15:26

17^F推cuylerLin: 阿，我自己都寫 C(4,3) 還乘錯www07/23 22:30

18^F→cuylerLin: 那就是 24 種沒錯07/23 22:30

[微積] 兩題偏微分問題

[ Math ]5 留言, 推噓總分: +2

作者: o11005 - 發表於 2020/07/20 23:21(5年前)

1^F推cuylerLin: 第一題請見以下圖片，有那裡打錯不清楚再跟我說XD07/21 00:52

2^F→cuylerLin: https://imgur.com/Ur7W4ns07/21 00:52

3^F推cuylerLin: 第二題的話不難，就代定義去算，不知道有沒有算錯07/21 01:10

4^F→cuylerLin: ，我計算分別是 0, x, 107/21 01:11

[中學] 分式除法討論

[ Math ]18 留言, 推噓總分: +3

作者: jac1471 - 發表於 2020/07/15 14:33(5年前)

1^F推cuylerLin: 當你寫下分式的時候就已經默認分母不為零了07/15 15:06

2^F→cuylerLin: 所以沒有什麼可不可為零的問題07/15 15:07

3^F→cuylerLin: 左邊第二項也可以先約掉一個x07/15 15:08

4^F→cuylerLin: 我是不知道現在國中高中教材怎麼樣啦07/15 15:11

5^F→cuylerLin: 還是依照教材為準，不要被扣分又說亂教XD07/15 15:11

6^F→cuylerLin: 如果不能約就全部寫出來而已，沒有什麼疑慮07/15 15:11

7^F→cuylerLin: 要約分就答案加註x的範圍07/15 15:11

12^F推cuylerLin: 我覺得要補上x不等於0跟307/15 15:35

[機統] 變異數觀念

[ Math ]16 留言, 推噓總分: +1

作者: pouttuiqoy - 發表於 2020/07/08 12:03(5年前)

2^F推cuylerLin: 定義就是這樣來的，變異數講的各資料點距離期望值的07/08 23:37

3^F→cuylerLin: 差距有多少，全部加起來作為一種資料分散性的指標07/08 23:37

4^F→cuylerLin: 這裡的距離就是一般的2-norm07/08 23:39

5^F→cuylerLin: 頂多在廣義機率測度的時候，把counting measure改成07/08 23:39

6^F→cuylerLin: 其他measure，但在怎麼樣都不會反映在你距離怎麼算07/08 23:39

7^F→cuylerLin: 除非你在某個奇怪的空間上定義特有的距離，例如採07/08 23:40

8^F→cuylerLin: 用geodistic來量(最短)距離，並在某個流形上有一個07/08 23:41

9^F→cuylerLin: 機率測度07/08 23:41

[機統] 一題貝式定理的疑問

[ Math ]4 留言, 推噓總分: +1

作者: MMaze - 發表於 2020/06/30 23:57(5年前)

1^F推cuylerLin: 沒有P(A)的條件？最多只能化簡到P(A)=P(AB)+P(AB^c)07/01 06:15

2^F→cuylerLin: 然後你再用cond.寫回去就可以得到07/01 06:15

3^F→cuylerLin: P(A|B^c)(1-P(B))=P(A)-P(A|B)P(B)，只剩P(A)未知07/01 06:16

[其他] 對偶問題

[ Math ]4 留言, 推噓總分: +1

作者: cloud777717 - 發表於 2020/06/23 22:23(5年前)

1^F推cuylerLin: 用Lagrangian來找對偶問題啊，然後主問題跟對偶問題06/23 22:38

2^F→cuylerLin: 只有在目標值相同時才會同時達到optimum，所以可能06/23 22:39

3^F→cuylerLin: 對偶問題比較好解(in a LP solver)06/23 22:40

4^F→cuylerLin: 可以轉成內積形式阿 ||x||^2=x'x, '是轉置06/23 23:34

[微積] 偏微觀念

[ Math ]1 留言, 推噓總分: 0

作者: lllll12b56 - 發表於 2020/06/21 12:23(5年前)

1^F→cuylerLin: f_x 和 f_y 是由一坨everywhere連續函數組合出來的06/22 22:45

[機統] 機率密度函數之分散和累積分布函數

[ Math ]4 留言, 推噓總分: +1

作者: MMaze - 發表於 2020/06/22 22:30(5年前)

1^F推cuylerLin: 阿你不是還少一個機率密度函數在support上積分要為106/22 22:43

2^F→cuylerLin: 的條件嗎？06/22 22:44

[線代] 請教一題線性代數

[ Math ]5 留言, 推噓總分: +1

作者: ac01965159 - 發表於 2020/06/22 20:36(5年前)

1^F推cuylerLin: (1)，考慮最小化 \norm{f(x)-\alpha g(x)} 的平方06/22 22:18

2^F→cuylerLin: 內積展開之後會是一個 quadratic form in \alpha06/22 22:19

3^F→cuylerLin: 對 \alpha 微分求極值就結束了06/22 22:19

4^F→cuylerLin: (2)，由(1)的結果直接把兩個函數帶進去求積分06/22 22:22

[機統] 常態分配

[ Math ]9 留言, 推噓總分: +4

作者: irpolo1 - 發表於 2020/06/14 23:36(5年前)

3^F推cuylerLin: 以第一題為例，後面兩題自己類推做法06/15 00:48

4^F→cuylerLin: 設M表示男生薪水，所求P(M>40,000)06/15 00:49

5^F→cuylerLin: =P((M-30000)/5000>(40000-30000)/5000)_06/15 00:50

6^F→cuylerLin: =P(Z>2)=0.02275 (查表)06/15 00:52

9^F→cuylerLin: 依照我的方法先列式，最後會需要查 z value06/18 22:17

首頁

尾頁