Re: [微積] 如何證明lim sinx/x=1如果面積概念未定義

看板Math作者 (Paul)時間10年前 (2015/02/23 00:58), 編輯推噓4(4推 0噓 15→)
留言19則, 3人參與, 最新討論串20/26 (看更多)
※ 引述《JohnMash (Paul)》之銘言： : ※ 引述《JohnMash (Paul)》之銘言： : : 本解法只用弧線長大於直線長及其類推 : : 來證明 : : http://imgur.com/ILy7jk1
: 鑑於上篇貼文對於若干不够嚴謹處 做了改寫 : 這樣就完成了 只用弧長不等式證明本題 : http://imgur.com/yeCnJf1
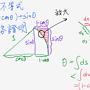
我們已知圓內接正2^n邊形的周長 在n趨於無窮大 其值趨於圓周長 因此可得 sinθ < θ <= sinθ + (1- cosθ) 因此 lim sin θ / θ = 1 我們的嚴格證明中 不用 ODE 不用 冪級數 不用面積分 不用Jacobian 請看附圖 http://imgur.com/5BSyMBv
-- Sent from my Android -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 123.194.229.234 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1424624336.A.5F2.html
推
02/23 01:02, , 1F
讚!
02/23 01:02, 1F
推
02/23 01:23, , 2F
所以前一次我提出所謂過不去的地方(ds還是曲線的
02/23 01:23, 2F
→
02/23 01:24, , 3F
那個證明)是真的過不去, 還是我哪裡誤會你的意思?
02/23 01:24, 3F
→
02/23 01:28, , 4F
你這證明沒用到圓面積公式,但用了扇形弧長公式S=rθ
02/23 01:28, 4F
→
02/23 01:28, , 5F
等同於用到圓周長公式，以及曲線弧長的定義
02/23 01:28, 5F
→
02/23 01:29, , 6F
還用到了「圓內接正2^n邊形的周長 在n趨於無窮大
02/23 01:29, 6F
→
02/23 01:29, , 7F
其值趨於圓周長」這件事
02/23 01:29, 7F
→
02/23 02:22, , 8F
Question: sin(theta/2)/(theta/2)=1?
02/23 02:22, 8F
→
02/23 02:23, , 9F
之前在夾時有用到
02/23 02:23, 9F
→
02/23 02:24, , 10F
另外，我會有點好奇alfadick你會不會對Apostol的
02/23 02:24, 10F
→
02/23 02:25, , 11F
Mathematical Analysis證明Bolzano-Weierstrass
02/23 02:25, 11F
→
02/23 02:25, , 12F
Theorem感到難以接受啊?
02/23 02:25, 12F
→
02/23 02:28, , 13F
我會提到是因為Apostol在證明Bolzano-Weierstrass
02/23 02:28, 13F
→
02/23 02:29, , 14F
也是在分割正方形喔
02/23 02:29, 14F
→
02/23 02:36, , 15F
那是不等式 JohnMash大沒說相等 而且sinx/x < 1已證
02/23 02:36, 15F
推
02/23 02:39, , 16F
ok，那我沒想到
02/23 02:39, 16F
→
02/23 08:29, , 17F
回yueayase,手上沒書,但分割正方形好像沒什麼問題?
02/23 08:29, 17F
推
02/24 00:16, , 18F
其實JohnMash這方法，和Steward的Apendix F應該是一
02/24 00:16, 18F
→
02/24 00:16, , 19F
樣的東西
02/24 00:16, 19F
‣ 更多 JohnMash 的文章
文章代碼(AID): #1KwWhGNo (Math)
討論串 (同標題文章)
本文引述了以下文章的的內容：
完整討論串 (本文為第 20 之 26 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共26篇)
‣ 更多 JohnMash 的文章
文章代碼(AID): #1KwWhGNo (Math)