Re: [微積] 如何證明lim sinx/x=1如果面積概念未定義

看板Math作者sippo ( )時間10年前 (2015/02/26 07:34)推噓2(2推 0噓 18→)

留言20則, 5人參與討論串24/26 (看更多)

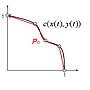
之前發過一篇文章解釋了為什麼 "表現良好" 的二維區域，其面積會跟線性尺度的平方成正比這篇要解釋的是，對 "表現良好" 的一維曲線線段，其弧長會跟線性尺度成正比考慮我們有一個線段兩端分別是 (1,0) 和 (0,1)，並可以參數化成 c(x(t), y(t)) 假設 c 滿足以下條件: (i) x(t) 連續，並在 [0,1] 單調遞減。 x(0)=1, x(T)=0 (ii) y(t) 連續，並在 [1,0] 單調遞增。 y(0)=0, y(T)=1 按照弧長的定義，我們可以對這個曲線用一組線段 Pn 作近似下圖中黑色是曲線，紅色是近似的線段 http://imgur.com/bUUphVV

Pn 的定義分成 n 段，第j段是把 ( x( (j-1)(T/n) ), y( (j-1)(T/n)) ) 和 ( x( (j)(T/n) ), y( (j)(T/n)) ) 以直線連接我們把第j段的長度稱為 |Pnj| n 弧長的定義是 lim Σ |Pnj| n->inf j=1 需要注意的是，弧長不一定存在: 當n趨近無窮大時，即使是固定區間，如果有無窮震盪，Pn 可能不會收歛。 * 接著我們考慮上面的曲線 c(x(t),y(t)) 因為 x(t), y(t) 單調遞減/遞增，在這個良好性質下可以證明更多東西首先考慮一系列的 {Pn}, n=2^k, k=1,2,... 由三角不等式，|P_n+1| >= |Pn|，因此 |Pn| 單調遞增。 |Pnj| <= (Pnj 在 x方向的投影長) + (Pnj 在 y方向的投影長) 因為 x(t), y(t) 單調遞減/遞增，對 j 加總後得知 |Pn| <= 2 因此，因為 |Pn| 單調遞增又有上界，弧長會收斂到一個定值。 * 得到曲線 c 的近似方法後，我們可以考慮相似形曲線 C(X(t), Y(t)) 其中 X(t) = a*x(t/a), Y(t) = a*y(t/a) c 跟 C 都可以做出各自的 Pn 來近似，兩者是成線性比例的因此弧長的極限值也會成線性比例。圓弧是這個證明中的特例，因此雖然我們沒有直接得到 pi，但是會知道圓弧跟半徑比會是一個固定常數 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 128.122.3.231 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1424907244.A.F5F.html ※ 編輯: sippo (128.122.3.231), 02/26/2015 08:57:24

推

yueayase

02/26 11:27, , 1^F

02/26 11:27, 1^F

→

yueayase

02/26 11:28, , 2^F

02/26 11:28, 2^F

推

gj942l41l4

02/26 12:03, , 3^F

02/26 12:03, 3^F