Re: [微積] 如何證明lim sinx/x=1如果面積概念未定義
※ 引述《sippo ( )》之銘言:
: 之前發過一篇文章解釋了為什麼 "表現良好" 的二維區域,
: 其面積會跟線性尺度的平方成正比
: 這篇要解釋的是,對 "表現良好" 的一維曲線線段,其弧長會跟線性尺度成正比
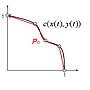
: 考慮我們有一個線段兩端分別是 (1,0) 和 (0,1),並可以參數化成 c(x(t), y(t))
: 假設 c 滿足以下條件:
: (i) x(t) 連續,並在 [0,1] 單調遞減。 x(0)=1, x(T)=0
: (ii) y(t) 連續,並在 [1,0] 單調遞增。 y(0)=0, y(T)=1
: 按照弧長的定義,我們可以對這個曲線用一組線段 Pn 作近似
: 下圖中黑色是曲線,紅色是近似的線段
: http://imgur.com/bUUphVV

: Pn 的定義分成 n 段,第j段是把 ( x( (j-1)(T/n) ), y( (j-1)(T/n)) )
: 和 ( x( (j)(T/n) ), y( (j)(T/n)) ) 以直線連接
: 我們把第j段的長度稱為 |Pnj|
發現這邊有個地方有點小問題, 只是我個人的小問題,
因為我們等等要去把圓寫成 (x(t),y(t)) 的東西,
然後用文章中的理論套進那裡去.
但我剛想了一下, 為什麼圓的曲線函數 (x(t), y(t)) 是連續的
也就是 x(t)=cosθ, y(t)=sinθ 為什麼是連續?
因為 lim sin x = sin c, 以及 lim cos x = cos c
x->c x->c
但這兩個是怎麼來的? 其實我不會證這個XDDD
大一微積分的書幾乎都省略這個 proof 了QQQ
我查到的書好像用了 |sinx|<=|x| 來證,
但|sinx|<=|x|怎麼證我只會用標準的證法──均值定理證, 由於MVT會用到微分,
所以用這種方式來證 |sinx|<=|x|, 接著來證 lim(x->c) sin x= sinc(即sin是連續函數)
來證明圓的 x(t) (以及y(t)) 是連續的, 進而套用之後的定理,
就會使我們的結果扯到三角函數的微分, 還是有點不太行的樣子~
ps: 我高度相信 lim sin x = sin c 很好證, 但我查不到有書有證XDD 我也不會證@_@
x->c
再跟你或其他版友要證明了~~
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 114.44.192.4
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1424957838.A.618.html
※ 編輯: alfadick (114.44.192.4), 02/26/2015 21:52:46
推
02/26 22:03, , 1F
02/26 22:03, 1F
→
02/26 22:04, , 2F
02/26 22:04, 2F
→
02/26 22:04, , 3F
02/26 22:04, 3F
→
02/26 22:33, , 4F
02/26 22:33, 4F
→
02/26 22:40, , 5F
02/26 22:40, 5F
→
02/26 22:42, , 6F
02/26 22:42, 6F
→
02/26 22:43, , 7F
02/26 22:43, 7F
→
02/26 22:44, , 8F
02/26 22:44, 8F
→
02/26 22:44, , 9F
02/26 22:44, 9F
→
02/26 23:10, , 10F
02/26 23:10, 10F
→
02/26 23:11, , 11F
02/26 23:11, 11F
→
02/26 23:14, , 12F
02/26 23:14, 12F
→
02/26 23:17, , 13F
02/26 23:17, 13F
→
02/26 23:22, , 14F
02/26 23:22, 14F
→
02/26 23:23, , 15F
02/26 23:23, 15F
→
02/26 23:23, , 16F
02/26 23:23, 16F
討論串 (同標題文章)
本文引述了以下文章的的內容:
完整討論串 (本文為第 25 之 26 篇):