作者查詢 / ipost

總覽項目：發文 | 留言 | 暱稱

作者 ipost 在 PTT [ Math ] 看板的留言(推文), 共93則

限定看板：Math

看板排序：

全部ComeHere346Math93movie91PC_Shopping11TW_Entertain10Eng-Class7Jacky_Woo6hardware5Option4EAseries2Hsinchu2Storage_Zone2<< 收起看板(12)

首頁

尾頁

Re: [中學] 國中數學

[ Math ]3 留言, 推噓總分: +1

作者: LPH66 - 發表於 2015/02/18 15:18(11年前)

1^F推ipost: 算到12(x-y)=x(x+1)時, 因x>x-y所以12>x+1就不需要02/18 22:34

2^F→ipost: 設 x=12k+8 了02/18 22:35

[中學] 好幾題看起來像是競賽型的題目

[ Math ]26 留言, 推噓總分: +18

作者: deardidi - 發表於 2015/02/15 07:37(11年前)

23^F推ipost: 16. 把一行或一列中的數全部減去一個常數, 再加上正02/16 12:24

24^F→ipost: 負和原矩陣的和相同. 先把每一列都減去最左邊的數,02/16 12:25

25^F→ipost: 再把每一行都減去該行最上面的數,得到全部為零的矩02/16 12:26

26^F→ipost: 陣, 所以總和是零.02/16 12:26

Re: [幾何] 多邊形內銳角的數量

[ Math ]8 留言, 推噓總分: +2

作者: XII - 發表於 2015/01/21 17:58(11年前)

6^F推ipost: 如果只是要得到這個上限用 1) x+y=n 2) 90*x+360*y01/22 08:49

7^F→ipost: > 180*(n-2) 就可以得到 3x<2n+4的結果. 用數學歸納01/22 08:50

8^F→ipost: 法構造的主要作用其實是證明了這個上限是tight01/22 08:50

Re: [中學] 國中幾何證明題

[ Math ]12 留言, 推噓總分: +2

作者: linkismet - 發表於 2014/12/03 10:07(11年前)

1^F推ipost: 式三那篇他在proposition 1和2有提到銳角,4雖然沒提12/05 08:52

2^F→ipost: 但原式因為沒有絕對值,他可能覺得很顯然是銳角不必12/05 08:53

3^F→ipost: 再說.坦白說如果要他補上範圍我覺得他會認為是吹毛12/05 08:55

4^F→ipost: 求疵12/05 08:55

5^F推ipost: 原式是說後面那篇的proposition 4抱歉沒看清楚我上12/05 11:35

6^F→ipost: 一篇的回文中猜測是式二有問題其實式二和式三導出12/05 11:36

7^F→ipost: 的過程我沒看也不清楚但不知道有無理解錯我覺得資12/05 11:36

8^F→ipost: 料庫的作者似乎認為式三可以推到鈍角的情形所以他12/05 11:37

9^F→ipost: 才加上絕對值現在您有一個證明說式三只限銳角我想12/05 11:38

10^F→ipost: 寄給他們去檢查怎比網友檢查要可靠吧?12/05 11:41

11^F→ipost: 怎比=總比12/05 11:42

Re: [中學] 國中幾何證明題

[ Math ]12 留言, 推噓總分: +5

作者: Sfly - 發表於 2014/11/30 11:42(11年前)

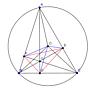
11^F推ipost: 因為BCEF共圓, 所以角AEF=角ABC. 2*角ABC+2*角OAC=12/01 09:55

12^F→ipost: 三角形ABC內角和=180度, 故角AEF+角OAC=90度得證12/01 09:56

Re: [中學] 國中幾何證明題

[ Math ]34 留言, 推噓總分: +7

作者: linkismet - 發表於 2014/11/29 11:21(11年前)

5^F推ipost: 有古典幾何證明: 設外心為O, BC中點為M, B對CO做垂11/30 11:19

6^F→ipost: 線垂足為H, 證明EF=BH. 因BEFHC共圓, 因此等於要證11/30 11:21

7^F→ipost: 明角BMH=角EMF. 因角EMF=180度-角A, 而角BMH=180度-11/30 11:23

8^F→ipost: 角A, 故得證. 然後DE和DF也如法炮製. 三角形面積=11/30 11:24

9^F→ipost: 1/2 R*(三頂點做AO BO CO的垂線)=1/2 R*(DF+DE+EF)11/30 11:25

10^F→ipost: 更正角BMH=角EMF=180度-2*角A11/30 11:27

11^F推ipost: 原題的等式好像對鈍角三角形不成立?11/30 12:51

12^F→ipost: 沒仔細看, 但是三角函數的證法有限定要銳角嗎?11/30 12:58

13^F→ipost: 如果式一式二式三對所有三角形都成立, 那顯然原11/30 13:31

14^F→ipost: 題對鈍角三角形也應該成立?11/30 13:32

20^F推ipost: 我覺得奇怪的是我和S大的證明初步看起來都無法適用11/30 18:39

21^F→ipost: 到鈍角也就是其實古典幾何證明並沒有證出鈍角的情11/30 18:40

22^F→ipost: 形而式二式三中用到了絕對值所以是有考慮到鈍角11/30 18:41

23^F→ipost: 的情形(內容我沒仔細看) 我在思考要怎麼把古典幾何11/30 18:43

24^F→ipost: 證明補完鈍角情形時, 發現鈍角好像是不成立的. 所以11/30 18:44

25^F→ipost: 要不就是鈍角的情形要另外想個古典證明, 要不就是那11/30 18:45

26^F→ipost: 三個三角函數公式有錯?11/30 18:45

27^F推ipost: 原命題對鈍角三角形不成立: 考慮一個等腰三角形,最11/30 19:09

28^F→ipost: 大角趨近180度, 則R趨近於無限大, 而DF+EF+FD趨近於11/30 19:10

29^F→ipost: 最大角對邊的兩倍11/30 19:11

30^F→ipost: 式二應該是針對銳角三角形但既然如此他在式中用絕12/01 09:29

31^F→ipost: 對值有何意義? XD12/01 09:31

[中學] 請教一題數學競試模擬題

[ Math ]17 留言, 推噓總分: +7

作者: LBJ66 - 發表於 2014/11/07 12:46(11年前)

3^F推ipost: 分五組比五次剩15匹拿五組第二名比一次取第一名剩711/07 13:30

4^F→ipost: 匹拿那匹和其他四組第一比剩下的再比一次應該8次11/07 13:32

5^F→ipost: 就可以吧11/07 13:33

6^F推ipost: 原題是問最少, 那就是7次就比出來11/07 13:35

7^F→ipost: 應該是問 "最多需要比幾次就一定知道前三名"11/07 13:36

10^F推ipost: 重排了一下, 最多不會超過七次. 第一次分五組, 第二11/07 14:45

11^F→ipost: 次拿五個第一比取前三, 剩六個, 然後除了第一名以外11/07 14:46

12^F→ipost: 五個再比一次.11/07 14:46

13^F推ipost: 六次不可能, 因為 25! > 5^611/07 14:51

14^F→ipost: 上面算錯了, 不知道6次可不可以11/07 14:53

[中學] 多項式

[ Math ]29 留言, 推噓總分: +7

作者: orz811017 - 發表於 2014/07/23 02:49(11年前)

1^F推ipost:用a=a'-1代入a^3+3a^2+4=0, 可以消掉平方項, 同理用07/23 10:33

2^F→ipost:b=b'-1代入, 然後兩式相加, (a'+b')=0是唯一實數解07/23 10:34

5^F推ipost:把它當成a'的二次方程式用判別式求b'範圍然後得知原07/23 22:28

6^F→ipost:三次式無解.07/23 22:29

9^F推ipost:你想反了.不是從三次方程式去得到D<0.如果要從三次方07/25 09:07

10^F→ipost:程式出發,畫個圖a' b'的解一正一負大概的範圍知道,很07/25 09:09

11^F→ipost:明顯另一個二次式會大於零.07/25 09:10

19^F推ipost:上面說以判別式求出b'的範圍然後得知原三次式無解07/26 10:54

20^F→ipost:判別式大於等於零, 所以 -2<=b'<=2,在這個範圍原三次07/26 10:56

21^F→ipost:小於0所以無解.07/26 11:00

22^F→ipost:原三次式指的是 b'^3-3b'-6=007/26 11:05

23^F→ipost:我的原話"以判別式求出b'的範圍然後得知原三次式無解07/26 11:05

24^F→ipost:我看不出來有什麼難了解的.如果你還是不明白也只好請07/26 11:07

25^F→ipost:你另請高明07/26 11:09

26^F推ipost:我想了一下,你的思考可能是有盲點,因為你也沒看出為07/26 11:23

27^F→ipost:什麼原三次方程式implies那個二次式會大於0.不知道你07/26 11:24

28^F→ipost:是鑽進了什麼牛角尖.07/26 11:25

[中學] 國中全等三角形

[ Math ]6 留言, 推噓總分: +1

作者: justin0602 - 發表於 2014/06/10 21:46(11年前)

4^F推ipost:ABC內找一點P使得角FDC等於角FCP且DC等於DP,P會在EF06/11 02:24

5^F→ipost:上故CF=PF BE=PE 得證06/11 02:25

6^F→ipost:更正是角FDC=角FDP06/11 11:29

Re: [中學] 競賽遊戲

[ Math ]8 留言, 推噓總分: +1

作者: diow1 - 發表於 2014/04/10 09:28(11年前)

1^F推ipost:答案是36次嗎?04/10 14:04

2^F→ipost:對任一數對(i,j),如果它們的起始位置和完成位置是反04/10 14:05

3^F→ipost:向的,則 "錯位數"加一, 所以本題有28個錯位.一次跳山04/10 14:06

4^F→ipost:會減少一個錯位數,所以需要至少28次跳山.連續幾次跳04/10 14:07

5^F→ipost:山後要一次平移才能再跳.當空格在偶數位可連跳山四次04/10 14:08

6^F→ipost:當空格在位置0或8可連跳四次,在位置1或7可連跳三次,04/10 14:09

7^F→ipost:所以跳法就是接連跳到不能跳,把空格平移一位,再連跳04/10 14:11

8^F→ipost:共28次跳山加上8次平移=36次04/10 14:12

首頁

尾頁