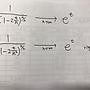看板
[ Math ]
討論串[微積] 極限
共 61 篇文章
內容預覽:
使用反證法 若 lim_(x->inf) f(x) 不為0. 則存在 c>0 使得 lim_(n->inf) f(nc) 也不為0. (Lemma) 給定任意 I = [a, b], 0 < a < b, 存在正整數 N 使得. 任意 J = [a', b'], N < a' < b. 皆存在一個正
(還有753個字)
內容預覽:
e 有很多定義方法. 根據你的問題我們採取以下流程:. (1) 證明 (1+1/n)^n 遞增有上界,因此實數公設說他是收斂的,定義為e. (2) 由(1)證明 lim (1+1/x)^x 亦為 e. x→+∞. (3) 由(2)與羅畢達證明 lim (1+1/x)^x 亦為 e. x→-∞. (相
(還有272個字)
內容預覽:
想問一題極限問題,如下圖,我從網路上看到的. 當n趨近無限大時,為什麼會變成exp(t)?. 那下面另一條也是如此嗎?. http://i.imgur.com/7ZhMLSX.jpg. 微積分有點弱,懇請大家幫忙解惑,謝謝大家. --. ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 223.
(還有346個字)