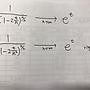Re: [微積] 極限
※ 引述《pp61022 (fight)》之銘言:
: 想問一題極限問題,如下圖,我從網路上看到的
: 當n趨近無限大時,為什麼會變成exp(t)?
: 那下面另一條也是如此嗎?
: http://i.imgur.com/7ZhMLSX.jpg

: 微積分有點弱,懇請大家幫忙解惑,謝謝大家
e 有很多定義方法
根據你的問題我們採取以下流程:
(1) 證明 (1+1/n)^n 遞增有上界,因此實數公設說他是收斂的,定義為e
(2) 由(1)證明 lim (1+1/x)^x 亦為 e
x→+∞
(3) 由(2)與羅畢達證明 lim (1+1/x)^x 亦為 e
x→-∞
(相當於證 lim (1-1/x)^x = 1/e )
x→+∞
(4) 由(2),(3) 證明 e^t = lim (1+t/x)^x , for all t€R
x→+-∞
再來就可以回答你的問題:
(一) 1/(1-2t/n)^(n/2) = 1/(1-t/(n/2))^(n/2) → 1/e^(-t) = e^t
(二) 1/(1-2t/n^2)^(n/2)
= 1/[(1-t/(n^2/2))^(n^2/2)]^(1/n) → 1/(e^(-t))^(1/n) = 1/1 = 1
嚴格說來,最後一步沒那麼嚴謹
你需要嚴格證明:if a_n → L > 0 then (a_n)^(1/n) → 1
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 111.255.4.42
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1491746107.A.712.html
推
04/09 23:19, , 1F
04/09 23:19, 1F
→
04/09 23:19, , 2F
04/09 23:19, 2F
討論串 (同標題文章)