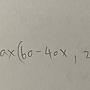作者查詢 / LPH66

總覽項目：發文 | 留言 | 暱稱

作者 LPH66 在 PTT [ Math ] 看板的留言(推文), 共8895則

限定看板：Math

看板排序：

全部Math8895C_and_CPP6694Minecraft2015puzzle1798Little-Games1256PHP992Web_Design736killercorp717java657SYSOP599Programming587Mathematica451Windows394IME389Prob_Solve389Ajax321RegExp298b94902xxx229PttBug229HOT_Game210Visual_Basic207Inference204Hunter198Steam168NTU-K9167KS94-317160EzHotKey138BoardGame131Conan122HarryPotter120CSSE116Flash104Database96GameDesign94AndroidDev91Android90Kindaichi_Q88Wikipedia74LaTeX71BBSmovie59SMSlife57DeathNote54riddle52Weyslii49wretch42IMO_Taiwan38Suckcomic38b96902HW37NTU37b94902HW35Doraemon30NTU-MAGIC26NTUDormM723NTUcourse21ONE_PIECE19b95902xxx18KSHS_Talk18b95902HW15NTNU_Lin_9615PLT15C_Chat14CSCouncil11PttCurrent11transgender9Translate-CS9VR9NTUDormG18Education7HSNU_10857KS93-3207NCKU-BEH957NDMC-D627PttNewhand7b99902HW6hikarugo6NtuDormM16youtuber6b96902xxx5b97902HW5CompilerDev5GO5L_LifeInfo5MJ5NSwitch5SummerCourse5tutor5Hsinchu4Liu4PushDoll4AppsForBBS3b98902HW3CSIE_WSLAB3Gossiping3Kao-KSHS3KS93-3163NARUTO3NTUST-DT93-23RSSH94_3013b97902xxx2ck50th3232ck55th3252ck58th3122CS_Badminton2CSIE_Mahjong2NANLIN3012NDHU-His962NTUDormFJr2NTUGIEE_EDA2PCman2PCSH91_3052PttSuggest2PttWeb2SFFamily2WinMine2Abin1AGO1Aquarius1Army-Sir1ASHS-93-li1AskaYang1B92310XXX1b99902xxx1blind_pc1Browsers1CCSH_92_3161CGU-MED-991CGU_EE981ck55th1201ck55th3241ck56th3181CK84Courage1CLHS-53-131CM38th071consumer1CPU_AM7011CPU_FC7311CSMU-MED941CTSH913021CTSH923051DaZhi6thH3021Eclipse1FJU-AM-901FJU-BA92C1FJU_GF1FSHS-94-3181Google1Grad-ProbAsk1Greenfield1HKday1Hoobastank1HORTUS-911HSNU_10731HSNU_9291HSNU_9381HSNU_9581HSNU_9851HSNU_9891HSNU_9901Hu_Yen_20041HY-40-Xin1ILSH-943131INSECT-901Itchie1Jay1JH30th3061Jinmen1joke1kekkai1KhalilFong1KS90-3091KS94-3151KS94-3211KS98-3021lab6211LD_IM93-21MATLAB1MDscience6th1Moto_GP1MuscleBeach1NCCU00_Stat1NCCU02_PSYCH1NCCU03_ETHNO1NCCU03_PF1NCCU04_MAT1NCCU04_Stat1NCCU98_RMI1NCCU99_Stat1NCHU-AGR001NCHU-AGR071NCKU-PH981NCUFingrad031Network1NIUECE911NTNU_bridge1NTOU-YP1NTPU-JLAW941NTPU_CK_CM1NTU-GIIB20021NTU-GIIB20041NTU95thLIS1NTUBIME-1021NTUCH-941NTUDormM61NTUE-Art961NTUE-CS1031NTUE_Nse961NTUE_Nse981NTUHistory881NTUHorti961NTUKGA1NTUMath911NTUMath941NTUMT-921NTUMystery1NTUNewPlace1NTUST-DT92-11NTUT_EE490A1NUTN_SSSS1Oguri_Shun1Old-Games1onlychild1Peitou29t3161Penny1PERCUSSION1PokeMon1PttHistory1Romances1RSSH93_3071SCU_ACCM971SM02th031SM05th3xx1SOFTSTAR1SSSH-13th3111STDM-87-3051Stephen1streetsinger1TFGCRC1THU-P-Softbo1TigerBlue1TMU9711Translation1TSH97_YK1Ur-hsing1VET_921w-inds1wegoJT3021WuLing46-3051WuLing46-3171YP91-3121YP92-3011YP92-3031YP94-3141<< 收起看板(252)

首頁

尾頁

[其他] 等價類形成分割，為何可以把重疊的類合併

[ Math ]54 留言, 推噓總分: +5

作者: alan23273850 - 發表於 2022/01/15 20:06(3年前)

20^F推LPH66: 等等, 這裡好像有點雞同鴨講01/16 23:30

21^F→LPH66: 你是想知道怎麼判定由兩個元素各別生成的等價類01/16 23:30

22^F→LPH66: 是互斥或全等「而已」, 還是想知道因此我們可以01/16 23:31

23^F→LPH66: 用一個元素代表一個等價類, 並由此得到 U' 集合?01/16 23:31

24^F→LPH66: 你文中的問題看起來像問前者01/16 23:32

25^F→LPH66: 但你後來又說想知道 U' 怎麼生出來的01/16 23:32

33^F推LPH66: 如果是這裡的話那就是 AoC: 給定許多等價類01/17 13:37

34^F→LPH66: (你應該知道每個等價類各都是一個集合)01/17 13:37

35^F→LPH66: AoC 表示我們可以在這 (可能無限多個) 等價類中01/17 13:37

36^F→LPH66: 每個集合各挑一個元素出來形成一個集合01/17 13:38

37^F→LPH66: 如果等價類只有有限多個那就是你說的有限多步搞定01/17 13:40

38^F→LPH66: 所以 AoC 只有在無限多個集合時才會用01/17 13:40

39^F→LPH66: 會不踏實的原因可能是因為選擇公理斷言存在的這個U'01/17 13:44

40^F→LPH66: 你寫不出來; 或者反過來說, 你寫不出來的這個 U'01/17 13:44

41^F→LPH66: 被選擇公理斷言存在01/17 13:44

44^F推LPH66: 那沒辦法, 選擇公理就是個這樣的東西01/20 00:25

45^F→LPH66: 它斷言一個選擇集合存在, 但在會用到它的狀況時01/20 00:26

46^F→LPH66: 我們基本上寫不出那個集合01/20 00:27

[中學] 一題排列組合

[ Math ]11 留言, 推噓總分: +1

作者: SC333 - 發表於 2022/01/18 18:30(3年前)

4^F推LPH66: 應該也不是敘述錯誤, 就只是單純的計算錯誤而已01/18 20:20

5^F→LPH66: 你的括號括成這樣造成你誤把三樓所述該加號放到外面01/18 20:21

6^F→LPH66: 實際上它仍然在大括號當中01/18 20:21

7^F→LPH66: 一般用排容的話會寫成 (全)-(取一)+(取二)-(取三)01/18 20:22

8^F→LPH66: 你寫成了 (全)-{(取一)-(取二)+(取三)}01/18 20:22

9^F→LPH66: 式子沒錯但當中間式子很長時, 運算符號在不在括號裡01/18 20:23

10^F→LPH66: 就容易搞錯01/18 20:23

11^F→LPH66: 可能因此算成 (全)-{(取一)-(取二)}+(取三) 就錯了01/18 20:24

[分析] 兩題有限元素分析求解

[ Math ]2 留言, 推噓總分: +1

作者: as0825 - 發表於 2022/01/12 15:59(3年前)

1^F推LPH66: 這個看起來比較像物理?01/12 21:27

[中學] 黃金矩形

[ Math ]4 留言, 推噓總分: +3

作者: SC333 - 發表於 2022/01/12 00:19(3年前)

1^F推LPH66: 角落的四個直角三角形有相似, 從他們出發算01/12 00:24

2^F推LPH66: 卡在什麼地方? 我看起來好像沒什麼卡的01/12 00:31

3^F推LPH66: 我的變數是設小段長度，正方形條件拿來列式01/12 00:50

4^F→LPH66: 然後多多運用黃金比的性質 φ^2=φ+101/12 00:52

[其他] minimize max pair

[ Math ]14 留言, 推噓總分: +6

作者: pipiLUANAIAI - 發表於 2022/01/08 13:52(3年前)

1^F推LPH66: 你式子沒寫完整: min() 裡面應該還有一項01/08 17:09

2^F→LPH66: 然後 min() 要等於什麼東西你也沒寫01/08 17:09

12^F推LPH66: 把六樓那個函數先畫出來 (應該會畫出上圖藍線)01/09 19:27

[其他] 資訊問題，謝謝大大

[ Math ]9 留言, 推噓總分: +1

作者: LKJX - 發表於 2022/01/04 11:37(3年前)

1^F推LPH66: 第一題, B 選項是三進位的每一位01/04 23:58

2^F→LPH66: 表示的方式是: 1=1, 2=3-1, 3=3, 4=3+1, 5=9-3-1 等01/04 23:59

3^F→LPH66: 由三進位特性以及這系列的"補"法可知它能連續表示到01/05 00:00

4^F→LPH66: 81+27+9+3+1=12101/05 00:00

5^F→LPH66: C 選項看似二進位, 但不是 64 而是 44, 總和僅 10701/05 00:01

6^F→LPH66: D 選項的五進位則沒辦法像三進位那樣用減的補01/05 00:01

7^F→LPH66: A E 兩選項容易發現不合01/05 00:02

8^F→LPH66: 第二題提示: 目標既然是要找全勝, 可嘗試把不會全勝01/05 00:04

9^F→LPH66: 的人給篩掉; 最後剩下一人時還要真的確認他是否全勝01/05 00:04

[中學] 中位數與眾位數的問題

[ Math ]15 留言, 推噓總分: +4

作者: mmxmmxmmx - 發表於 2021/12/15 16:08(4年前)

11^F推LPH66: 是「資料筆數」不是「資料組數」12/16 12:45

12^F→LPH66: 這裡的資料是 7,7,7,7,7,8,8,8,9,10,10,10,10,10,12/16 12:46

13^F→LPH66: 10,10,10,11,11,11,11 在這些資料數裡去找正中間12/16 12:46

[線代] 線性獨立的問題

[ Math ]9 留言, 推噓總分: +4

作者: harry921129 - 發表於 2021/12/14 12:31(4年前)

3^F推LPH66: 你的條件相當於 a b c 三向量皆與 (x',y',z',u')12/14 23:43

4^F→LPH66: 內積為 0, 由此你容易能找到一組不線性獨立的三向量12/14 23:45

5^F推LPH66: 你的後一個問題是把變數弄反了, 你的變數是 a b c12/14 23:48

6^F→LPH66: x y z u 是已知數, 因此你不能套用它們是變數的結論12/14 23:48

7^F→LPH66: 另外你也用錯東西了: 你式子右邊是零向量12/15 00:00

8^F→LPH66: 那個比較像是在討論 kernel 和 nullity 的式子12/15 00:01

9^F→LPH66: 和 rank 正好是互相反過來的東西12/15 00:02

Re: [其他] 關於時間複雜度（big O）的排序

[ Math ]1 留言, 推噓總分: +1

作者: arrenwu - 發表於 2021/12/14 10:44(4年前)

1^F推LPH66: 我比較喜歡兩邊取 log 之後記 log(N!) = O(N log N)12/14 11:56

Re: [代數] 問一題模考的多項式

[ Math ]11 留言, 推噓總分: +5

作者: LimSinE - 發表於 2021/12/03 21:15(4年前)

7^F推LPH66: 那條必要條件可以乘 4 變形為 (2B+1)^2 = 2^(d+2)-712/04 00:05

8^F→LPH66: 右邊這東西要恰好踩到一個奇完全平方數...12/04 00:05

10^F推LPH66: 所以這五解就真的是僅有的五解 wow12/04 11:00

首頁

尾頁