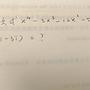討論串(共102篇) - [中學] 多項式 - 看板Math

看板 [ Math ]

討論串[中學] 多項式

共 102 篇文章

排序：最新先 | 最舊先 | 留言數 | 推文總分

內容預覽：開啟 | 關閉 | 只限未讀

推噓2(2推 )留言17則，0人參與, 7年前最新作者Mistouko (Mistouko)時間7年前 (2018/01/18 03:21)資訊

內容預覽:

題目：設函數 f(x)=x(x+1)(x-2)+0.01 的圖形與x軸交於. A(a,0)、B(b,0)、C(c,0) 三點，且 g(x)=-x(x+1)(x-2)+0.01. ，下列哪些選項正確？. (A) a+b+c>0. (B) abc>0. (C) 函數g(x)的圖形與x軸交於三點. (D)

(還有184個字)

#86

Re: [中學] 多項式

推噓0(0推 )留言0則，0人參與作者aromaQ626 (摳咪霉庇)時間8年前 (2017/07/22 13:18)資訊

內容預覽:

1 - 3i 另一共軛虛根為 1 + 3i. 為 x^2 - 2x + 10 = 0 之兩根. 原式 x^4 - 3x^3 - 12x^2 - 5x - 6. = ( x^2 - 2x + 10 )( x^2 - x - 24 ) + ( -43x + 234 ). f(1 - 3i). = -43

(還有89個字)

#85

[中學] 多項式

推噓2(2推 )留言5則，0人參與作者tony890415 (tony)時間8年前發表 (2017/07/22 11:58), 8年前編輯資訊

內容預覽:

http://i.imgur.com/rBLTAoF.jpg. 目前想到用余式定理解. 但沒什麼進一步想法. 謝謝. --. ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 101.139.136.110. ※ 文章網址: https://www.ptt.cc/bbs/Math/M.15007

#84

[中學] 多項式

推噓0(0推 )留言3則，0人參與作者susiseptem (..)時間9年前 (2016/11/04 16:59)資訊

內容預覽:

設多項式f(x)除以 3x+1的商數為Q(x) 餘式是5 試求(x-1)f(x/3) 除以x+1的商數和餘數. 感恩^^. --. ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 36.229.214.45. ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1478

#83

Re: [中學] 多項式

推噓0(0推 )留言0則，0人參與作者Eliphalet (重感冒中)時間9年前 (2016/03/28 02:22)資訊

內容預覽:

x p(x-1) = (x-10) p(x)；代入 x = 0 可知 p(0) = 0；代入 x = 1 可知 p(1) = 0. ... 到 p(9) = 0. 因此我們可以令 p(x) = x(x-1)(x-2)...(x-9)q(x) -(*). 現在把 (*) 代回原式可得. q(x-1)

(還有14個字)

首頁

尾頁