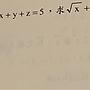Re: [中學] 柯西不等式
※ 引述《hiu (閉門造愛)》之銘言:
: a和b皆為正實數,且a+b=1。求 ( a + 1/a )^2 + ( b + 1/b )^2 的最小值
: 請問有沒有微分以外的方法?
: 是否可以用柯西不等式來解呢?
: 謝謝各位大大~
(a + 1/a)^2 + (b + 1/b)^2 >= (1/2)[a + 1/a + b + 1/b]^2
= (1/2)[1 + 1/ab]^2
>= 25/2,此為最小值
等號成立在a + 1/a = b + 1/b
=> (a - b)[1 - 1/ab] = 0
=> 只有a = b的可能
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 117.56.175.175 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1684874544.A.261.html
討論串 (同標題文章)