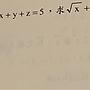[中學] 柯西不等式

看板Math作者 (閉門造愛)時間2年前 (2023/05/24 02:58), 編輯推噓2(2推 0噓 6→)
留言8則, 2人參與, 2年前最新討論串19/22 (看更多)
a和b皆為正實數，且a+b=1。求 ( a + 1/a )^2 + ( b + 1/b )^2 的最小值 請問有沒有微分以外的方法? 是否可以用柯西不等式來解呢? 謝謝各位大大~ -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 1.160.3.46 (臺灣) ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1684868319.A.D65.html
推
05/24 03:42, 2年前 , 1F
原式=a2 +b2 +(1/a2 )+(1/b2 )+4=(a2 +b2 )+(a2 +b2
05/24 03:42, 1F
→
05/24 03:42, 2年前 , 2F
+4=(1-2ab)+1/(ab)2 -2/(ab)+4
05/24 03:42, 2F
→
05/24 03:42, 2年前 , 3F
=
05/24 03:42, 3F
→
05/24 03:43, 2年前 , 4F
上面的推文忽略 不小心送出
05/24 03:43, 4F
→
05/24 04:05, 2年前 , 5F
05/24 04:05, 5F
推
05/24 18:29, 2年前 , 6F
樓上原本的算式可以變成 (1-2ab)(1+(ab)^-2)，他隨
05/24 18:29, 6F
→
05/24 18:30, 2年前 , 7F
ab 的增加而減少，所以我們要找的是 ab 的最大值。
05/24 18:30, 7F
→
05/24 19:49, 2年前 , 8F
還差一個+4，不過最後再補上就好。
05/24 19:49, 8F
‣ 更多 hiu 的文章
文章代碼(AID): #1aRGpVrb (Math)
討論串 (同標題文章)
以下文章回應了本文：
完整討論串 (本文為第 19 之 22 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共22篇)
‣ 更多 hiu 的文章
文章代碼(AID): #1aRGpVrb (Math)