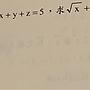Re: [中學] 柯西不等式

看板Math作者 (生命中無法承受之輕)時間8年前 (2017/12/05 22:50), 編輯推噓1(1推 0噓 5→)
留言6則, 2人參與, 8年前最新討論串11/22 (看更多)
※ 引述《semmy214 (黃小六)》之銘言： : https://imgur.com/a/qVcLP : 這題感覺是進階題 : 請瞭解的大大詳解~3Q 由柯西不等式知 (1^2 + z^2)[(x+y)^2 + 1^2] >=(x+y+z)^2 又由題意知 (x+y+z)^2 = (1+z^2)[ 1+(1+x^2)(1+y^2) ] 故 (1^2 + z^2)[(x+y)^2 + 1^2] >=(1+z^2)[ 1+(1+x^2)(1+y^2) ] => [(x+y)^2 + 1^2]>=[ 1+(1+x^2)(1+y^2) ] => x^2 + 2xy + y^2 + 1 >= 1 + 1 + x^2 + y^2 + (xy)^2 => (xy-1)^2 <= 0 , 故 xy = 1 => y = 1/x 柯西等號成立時, 1/(x+y) = z/1 => z = 1/(x+y)= 1/[x+(1/x)] = x/(1+x^2) 故f(x)=1/x, g(x)=x/(1+x^2)_ -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 36.239.25.199 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1512485420.A.5B4.html
推
12/06 08:19, 8年前 , 1F
一樣的技術可以用兩次啊
12/06 08:19, 1F
→
12/06 08:20, 8年前 , 2F
(1+z^2)(1+(x^2+1)(1+y^2))
12/06 08:20, 2F
→
12/06 08:21, 8年前 , 3F
>= (1+z^2)(1+(x+y)^2) >= (x+y+z)^2
12/06 08:21, 3F
→
12/06 09:03, 8年前 , 4F
請問D大(1+(x^2+1)(1+y^2)) >= 1 + (x+y)^2怎麼算?
12/06 09:03, 4F
→
12/06 09:12, 8年前 , 5F
(x^2+1^2)(1^2+y^2) >= (x 1+1 y)^2
12/06 09:12, 5F
→
12/06 09:56, 8年前 , 6F
><抱歉問了這種蠢問題
12/06 09:56, 6F
‣ 更多 tzhau 的文章
文章代碼(AID): #1Q9h8iMq (Math)
討論串 (同標題文章)
本文引述了以下文章的的內容：
完整討論串 (本文為第 11 之 22 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共22篇)
‣ 更多 tzhau 的文章
文章代碼(AID): #1Q9h8iMq (Math)