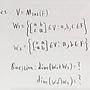作者查詢 / zako1113

總覽項目：發文 | 留言 | 暱稱

作者 zako1113 在 PTT [ Math ] 看板的留言(推文), 共146則

限定看板：Math

看板排序：

首頁

尾頁

[線代] 矩陣維度問題

[ Math ]9 留言, 推噓總分: +2

作者: a32905169 - 發表於 2018/05/08 01:52(7年前)

7^F推zako1113: dim(V)=4, dim(W1)=3, dim(W2)=2, W2有W1沒有的元素05/08 04:15

8^F→zako1113: , 所以4>=dim(W1+W2)>3, 只能是405/08 04:15

9^F→zako1113: 然後dim(W1+W2)=dim(W1)+dim(W2)-dim(W1∩W2)算05/08 04:17

[分析] 請推薦O.D.E.的專書

[ Math ]14 留言, 推噓總分: +4

作者: cyt147 - 發表於 2018/03/02 08:32(8年前)

9^F推zako1113: Kreyszig, Introductory Functional Analysis with03/04 00:39

10^F→zako1113: Applicationn, section 5.303/04 00:40

11^F→zako1113: Apostol的練習也不是沒用uniform convergence03/04 00:43

12^F→zako1113: 因為uniform convergence就是sup norm convergence03/04 00:44

13^F→zako1113: 那個練習題目就有寫用sup norm做了03/04 00:45

LS soln w semi norm

[ Math ]10 留言, 推噓總分: +5

作者: saltlake - 發表於 2017/12/15 22:00(8年前)

1^F推zako1113: inv(A'A + c^2 L'L) A' b ' 指 transpose12/15 23:32

2^F推zako1113: https://goo.gl/M9TEQA12/16 03:50

3^F推zako1113: 應該沒類似的式吧 L跟A的singular vector不同12/16 10:13

4^F推zako1113: Matrix Computation (4th Ed) by Gene H. Golub12/16 13:21

5^F→zako1113: 6.1.5和6.1.6有用GSVD寫的公式要L是invertible12/16 13:22

8^F推zako1113: 不是GSVD要L是可逆, 是要寫regularized soln時要的12/16 19:34

9^F→zako1113: 要 L 是可逆似乎是要讓 L 沒有 zero singular value12/16 19:42

10^F→zako1113: 確保那個類似 A'A + c^2L'L 的矩陣是正定->有唯一解12/16 19:44

[其他] 微分方程

[ Math ]10 留言, 推噓總分: +1

作者: CNN0538 - 發表於 2017/01/05 20:17(9年前)

1^F推zako1113: 最首先平方之後已經不是線性微分方程01/05 20:33

[分析] 一個Delta Function的積分

[ Math ]16 留言, 推噓總分: +3

作者: uni1021 - 發表於 2016/10/25 17:40(9年前)

11^F推zako1113: 這個distribution不是機率分佈10/25 19:41

12^F→zako1113: 而是generalized function10/25 19:42

[分析] 怎麼理解interval(0,1)為不可數

[ Math ]16 留言, 推噓總分: +5

作者: Remedy - 發表於 2016/10/15 17:50(9年前)

1^F推zako1113: 沒有bijective function由N到(0,1)10/15 18:17

[分析] bounded variation

[ Math ]2 留言, 推噓總分: +1

作者: DC40 - 發表於 2016/09/25 19:56(9年前)

1^F推zako1113: 題目有uniform bound M, 反例沒這條件09/25 20:14

[其他] 我不確定這算什麼問題

[ Math ]2 留言, 推噓總分: +1

作者: jass970991 - 發表於 2016/07/05 11:19(9年前)

1^F推zako1113: lebesgue integral, hausdorff measure07/05 14:26

[微積] 定積分

[ Math ]7 留言, 推噓總分: +2

作者: ffej8797 - 發表於 2016/06/28 10:28(9年前)

3^F推zako1113: cos(x)-sin(x) = sqrt(2)*sin(pi/4-x) 是在pi/4對06/28 11:06

4^F→zako1113: 稱的奇函數06/28 11:06

5^F推zako1113: 加了^2015後亦然, 所以大概可以用u=x-pi/4, 變成-pi06/28 11:09

6^F→zako1113: /4到pi/4的積分後再證要積的是奇函數06/28 11:09

Re: [線代] Sparse近似最佳化問題

[ Math ]14 留言, 推噓總分: +4

作者: abc2090614 - 發表於 2016/06/17 10:54(9年前)

6^F推zako1113: 可以看一下 http://www.imm.dtu.dk/~pcha/Regutools06/17 18:20

7^F→zako1113: Complete manual (pdf file) 的5-6頁06/17 18:20

8^F→zako1113: 就是當A的condition number大的時候, 解Ax=b是很06/17 18:21

9^F→zako1113: unstable的, 通常是A會把高頻的input消去06/17 18:22

10^F→zako1113: 而作LSQ解的時候就會相反, 把高頻的noise放大06/17 18:23

11^F→zako1113: 所以b有誤差的時候直接的LSQ解也沒用06/17 18:24

首頁

尾頁