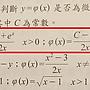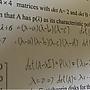作者查詢 / Vulpix

總覽項目：發文 | 留言 | 暱稱

作者 Vulpix 在 PTT [ Math ] 看板的留言(推文), 共7171則

限定看板：Math

看板排序：

全部C_Chat39862Math7171movie2397Militarylife1813Physics1688tutor645C_ChatBM570AI_Art512NTU426CS_TEACHER331ck57th317223IdolMaster210gymnastics185Army-Sir148ProjectSekai88MP78HomeTeach67WataseYuu65ProjectKondo58give48Hunter43Gossiping39Line_OPTC39NIHONGO39TamShui39LerraBattle36Conan33ck-talk32LightNovel29NARUTO17Google16NTUSA16The-fighting15ck57th31513L_LifePlan13book12Comic12NTUcourse12Statistics12KS98-30211phys9411StupidClown10joke9NSwitch9WATARU9Detective8Marginalman8Seiya7PokeMon6SENIORHIGH6CFantasy5Disney5Doraemon5JinYong5TypeMoon5gallantry4historia4Shana4Suckcomic4TWvoice4X_Z_Zhou4About_Clubs3EYESHIELD213Food3KOF3L_HappyLivin3LAW3ONE_PIECE3WOW3Wrestle3AntiVirus2AudioPlayer2C_BOO2C_GenreBoard2C_Question2ChineseTeach2ck57th3302ck61st3222CVS2CyberFormula2Falcom2GirlComics2HatePolitics2kenichi2Kojima2LittleFight2mobile-game2NTUJapan062Old-Games2PlayStation2RumikoTWorld2specialman2Teacher2Tokusatsu2Tyukaitiban2Vtuber2ADS1Animation1ArakawaCow1AVEncode1BLEACH1Childhood1ck54th3101ck57th3011ck57th3211ck59th3121DummyHistory1EAseries1Fantasy1FATE_GO1GameDesign1Handiwork1Hate1HitmanReborn1home-sale1Jacky1JAM_Project1JP_Entertain1KS94-3071Lions1LoveLive1Native1NTHUMathG1NTU-Exam1NTU_4H_Club1Office1Olympics_ISG1Palmar_Drama1part-time1pet1phys931Precure1Railway1RIVER1SAN1share1Shokugeki1SKET_DANCE1SouthPark1streetfight1TakahashiRie1Tech_Job1trans_math1TW-language1UmaMusume1Yakitate1<< 收起看板(146)

首頁

尾頁

[微積] 各位大大不知道我這樣證明可以嗎

[ Math ]2 留言, 推噓總分: +1

作者: max93765 - 發表於 2019/04/29 11:40(6年前)

1^F→Vulpix: 因為教授內建自動排版功能，還會腦補連接詞。04/29 12:49

Re: [其他] 對某段時間平均之變數的常微方

[ Math ]8 留言, 推噓總分: 0

作者: saltlake - 發表於 2019/04/28 07:27(6年前)

1^F→Vulpix: 反正你對 s 做的事情又不影響對 t 的微分。04/28 08:16

2^F→Vulpix: 誒，不對，g 本來是單變數函數 g(t)，不能突然變成04/28 08:25

3^F→Vulpix: g(t,tt) 這樣的雙變數函數吧。04/28 08:25

4^F→Vulpix: 我猜你想寫的是：int( g(t+tt), tt = 0 to s)/s04/28 08:25

5^F→Vulpix: 那這樣還是一個捲積喔。還有你誤會了，捲積後函數只04/28 08:26

6^F→Vulpix: 會更平滑，gbar 至少也會像 g 一樣光滑，而不會是04/28 08:28

7^F→Vulpix: 片段線性函數。04/28 08:28

8^F→Vulpix: 然後是最後一個問題，答案：是。(a 是常數的話。)04/28 08:31

[微積] ln|x|微分，x<0 的疑問

[ Math ]26 留言, 推噓總分: +6

作者: yiting428 - 發表於 2019/04/27 00:59(6年前)

1^F推Vulpix: ln。abs 左半支的斜率都是負的呀？04/27 01:02

4^F推Vulpix: 不正確(但很普遍)。因果關係不對。04/27 02:45

5^F→Vulpix: 如果你的課本用 ∫_1^x dt/t 來定義 ln(x)，那你應04/27 02:48

6^F→Vulpix: 那你應該從 ∫_{-1}^x dt/t 來思考，首先 x>0 是沒04/27 02:50

7^F→Vulpix: 有意義的，因為會跨過 1/x 的奇點(x=0)。x=0 也一樣04/27 02:52

8^F→Vulpix: 無意義，所以僅考慮 x<0。而從積分的定義，顯然04/27 02:53

9^F→Vulpix: ∫_{-1}^x dt/t = ∫_1^{-x} ds/s，其中 s=-t。04/27 02:56

10^F→Vulpix: 所以 ∫_{-1}^x dt/t = ∫_1^{-x} ds/s = ln(-x)。04/27 02:56

11^F→Vulpix: 因此 ∫dx/x 這個不定積分，在 x>0 時會積出 ln(x)04/27 02:59

12^F→Vulpix: +C，而在 x<0 時則是 ln(-x)+D，其中 C、D 都是常數04/27 03:00

13^F→Vulpix: 幾乎在所有的用途上，都不會遇到跨越 x=0 的積分，04/27 03:01

14^F→Vulpix: 所以 C、D 可能不同這件事顯得很不重要，都寫成 C。04/27 03:02

15^F→Vulpix: 所以積分表上的公式才是：∫dx/x = ln|x| + C。04/27 03:03

18^F推Vulpix: 目前 ln(負數) 是不存在沒錯。不過有一天你有可能04/28 01:15

19^F→Vulpix: 會需要，那時候自然會去定一個符合當下需求的定義。04/28 01:16

24^F→Vulpix: 其實還是 ∫_1^x dt/t 啦XD 只是積分路徑在複數平04/28 01:20

25^F→Vulpix: 面上繞來繞去的而已。ln 的本質確實是 1/x 的反導04/28 01:21

26^F→Vulpix: 函數。04/28 01:21

Re: [代數] 請求詳細的過程

[ Math ]5 留言, 推噓總分: +3

作者: Desperato - 發表於 2019/04/27 19:11(6年前)

3^F推Vulpix: The Frobenius map is an endomorphism, which fix04/27 22:11

4^F→Vulpix: GF2 in GF8[x].04/27 22:12

[微積] 基本微分方程一題

[ Math ]5 留言, 推噓總分: +2

作者: yiting428 - 發表於 2019/04/24 22:47(6年前)

2^F→Vulpix: 你該不會是C差了一個負號？04/26 02:19

3^F推Vulpix: 答案寫錯啦。04/26 23:40

4^F→Vulpix: 市售的高等教育中文數學書通常都很多錯誤，驗算才是04/26 23:44

5^F→Vulpix: 正途。04/26 23:44

[分析] 傅立葉轉換小問題

[ Math ]2 留言, 推噓總分: +1

作者: NTUmaki - 發表於 2019/04/26 18:44(6年前)

1^F推Vulpix: 是啊。04/26 23:42

[中學] 多項式

[ Math ]12 留言, 推噓總分: +3

作者: testishard - 發表於 2019/04/26 15:43(6年前)

2^F推Vulpix: 1^2-1+a 也會整除 1^13+1+90，你再想想看其他x。04/26 16:00

3^F→Vulpix: 候選的a，一隻手就能數完。04/26 16:01

5^F→Vulpix: x=0 試過沒？04/26 16:18

9^F→Vulpix: 不過這個作法其實需要Gauss Lemma，高中都不提。04/26 17:44

[線代] 行列式、特徵值問題請益

[ Math ]11 留言, 推噓總分: +3

作者: a4567567 - 發表於 2019/04/24 16:15(6年前)

1^F推Vulpix: 教授的p(λ)=det(λI-A)，但他以為是det(A-λI)。04/24 16:46

[中學] 組合式的組合解釋

[ Math ]1 留言, 推噓總分: 0

作者: LKJX - 發表於 2019/04/23 11:38(6年前)

1^F→Vulpix: 先不論有公式被打錯，只要是組合公式就都會有解釋。04/23 15:04

[其他] 對某段時間平均之變數的常微方

[ Math ]4 留言, 推噓總分: +2

作者: saltlake - 發表於 2019/04/23 06:10(6年前)

2^F推Vulpix: 你想做的是做了捲積後的y的ODE，那就考慮Fourier轉04/23 13:15

3^F→Vulpix: 換，大概就能把y解出來。如果你想要一個這些手段都04/23 13:15

4^F→Vulpix: 沒有用的，那就是數值解啊。04/23 13:15

首頁

尾頁