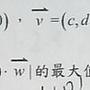[中學] 空間向量

看板Math作者 (batmen)時間11年前 (2014/06/13 10:44), 編輯推噓1(1推 0噓 7→)
留言8則, 2人參與, 最新討論串9/35 (看更多)
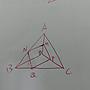
因為沒有圖所以只好用打的 空間中有兩個三角形ABC與A'BC形成的兩面角為60度 D,E分別為其中一三角形AC,AB的中點 F,G分別為其中一三角形A'C,A'B的中點 想問的是該如何證明 其中DEFG會是一個長方形呢? 我有想過三垂線定理不過不確定 另外想問的是若是今天兩面角不是60度,那空間中DEFG仍然會是一個長方形嗎? 謝謝!! -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 114.40.84.36 ※ 文章網址: http://www.ptt.cc/bbs/Math/M.1402627457.A.058.html
推
06/13 11:10, , 1F
三垂線即足夠了, 考慮 D 到平面 A'BC 的垂足 D'
06/13 11:10, 1F
→
06/13 11:10, , 2F
在平面 A'BC 上作一直線 L 過 D' 與 BC 垂直
06/13 11:10, 2F
→
06/13 11:11, , 3F
則 L 垂直 FG 且因 L 在平面 A'BC 上故 L 垂直 DD'
06/13 11:11, 3F
→
06/13 11:12, , 4F
簡單的投影法又可證 L 與 FG 的交點即為 F
06/13 11:12, 4F
→
06/13 11:13, , 5F
再由三垂線即知 DF 垂直 FG 其他三個角類似
06/13 11:13, 5F
→
06/13 11:14, , 6F
唔等等, 四樓好像要 ABC 全等 A'BC 才能成立...
06/13 11:14, 6F
→
06/13 11:14, , 7F
另外以上證明跟兩面角度數無關
06/13 11:14, 7F
→
06/13 16:57, , 8F
了解!另外忘了附上那三角形都是正三角形才對 感恩~
06/13 16:57, 8F
‣ 更多 batmen 的文章
文章代碼(AID): #1JccM11O (Math)
討論串 (同標題文章)
以下文章回應了本文：
完整討論串 (本文為第 9 之 35 篇)：
排序： 最新先 | 最舊先 | 留言數
中學
0
5
[中學] 空間向量 空間向量
fess
7年前, 01/18
在新視窗開啟完整討論串 (共35篇)
‣ 更多 batmen 的文章
文章代碼(AID): #1JccM11O (Math)