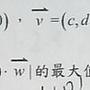Re: [中學] 空間向量
※ 引述《jewry2005 (猶太)》之銘言:
: ※ 引述《zi98btcc (幼斤)》之銘言:
: [(a+2b+3c-1)^2+(2a+b+3c-1)^2+(3a-b+2c-1)^2](p^2+q^2+r^2)≧
: [(a+2b+3c-1)*p+(2a+b+3c-1)*q+(3a-b+2c-1)*r]^2
: (a+2b+3c-1)*p+(2a+b+3c-1)*q+(3a-b+2c-1)*r
: = (p+2q+3r)a + (2p+q-r)b + (3p+3q+2r)c - (p+q+r)
: 任何實數p、q、r都會使這個不等式成立,
: 當a、b、c係數都為0時也成立,這是一個技巧
: p + 2q + 3r = 0
: 2p + q - r = 0
: 3c + 3q + 2r = 0
: 不用外積,一樣可以解出p、q、r的比例,
: 我倒覺的a大這手很漂亮。
一般柯西不等式如下,
(a1^2+a2^2)(b1^2+b2^2)≧(a1b1+a2b2)^2
(a1 a2 b1 b2)4個變數的不等式
(a1^2+a2^2+a3^2)(b1^2+b2^2+b3^2)≧(a1b1+a2b2+a3b3)^2
(a1 a2 a3 b1 b2 b3)6個變數的不等式
(a1^2+a2^2+a3^2+a4^2)(b1^2+b2^2+b3^2+b4^2)≧(a1b1+a2b2+a3b3+a4b4)^2
(a1 a2 a3 a4 b1 b2 b3 b4)8個變數的不等式
..............................................
以 (a1^2+a2^2+a3^2)(b1^2+b2^2+b3^2)≧(a1b1+a2b2+a3b3)^2 為例,
如果加上 1 個限制條件:b1=k*a1,上式可改為
(a1^2+a2^2+a3^2)((k*a1)^2+b2^2+b3^2)≧(a1(k*a1)+a2b2+a3b3)^2
變成(a1 a2 a3 b2 b3)5個變數的不等式
如果加上 3 個限制條件:b1=k*a1,b2=k*a2,b3=k*a3,上式可改為
(a1^2+a2^2+a3^2)((k*a1)^2+(k*a2)^2+(k*a3)^2)=(a1(k*a1)+a2(k*a2)+a3(k*a3))^2
變成(a1 a2 a3)3個變數的等式,整理一下即
k^2*(a1^2+a2^2+a3^2)^2=k^2*(a1^2+a2^2+a3^2)^2
這等式當中(a1 a2 a3)可自由為任何一組實數,並不會限制在某範圍,如
a1+a2+a3=0 或 a1-2a2-3a3=0,不會限制在左式
同樣的道理,
[(a+2b+3c-1)^2+(2a+b+3c-1)^2+(3a-b+2c-1)^2](p^2+q^2+r^2)≧
[(a+2b+3c-1)*p+(2a+b+3c-1)*q+(3a-b+2c-1)*r]^2=
[(p+2q+3r)a+(2p+q-r)b+(3p+3q+2r)c-(p+q+r)]^2
可視為(a b c p q r)6個變數的不等式,
如果加上 3 個限制條件:p=k*(a+2b+3c-1),q=k*(2a+b+3c-1),r=k*(3a-b+2c-1),
一樣變成(a b c)或(p q r)3個變數的等式如下,
k^2*[(a+2b+3c-1)^2+(2a+b+3c-1)^2+(3a-b+2c-1)^2]^2=
k^2*[(a+2b+3c-1)^2+(2a+b+3c-1)^2+(3a-b+2c-1)^2]^2
沒有理由會得到聯立方程式
p + 2q + 3r = 0
2p + q - r = 0
3p + 3q + 2r = 0
3個變數的等式當中(p q r)是自由的,也可以是
p + 2q + 3r = 6
2p + q - r = 2
3p + 3q + 2r = 8
為何不能選這組聯立方程式呢?
雖然 p + 2q + 3r = 0
2p + q - r = 0
3p + 3q + 2r = 0
是正確的,但來源從何而來?
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 49.158.186.133
推
05/24 08:29, , 1F
05/24 08:29, 1F
討論串 (同標題文章)