
Re: [中學] 不要太依賴chatgpt

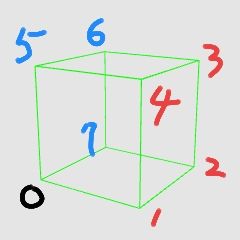
: : 設O為(0,0,0)
: : 考量X軸情況:
: : PQ兩點共有C7取2種可能,
: : 但只有紅色C4取2的情況,
: : X軸內積和才為1,
: : 其餘皆為0
: : 所以X軸期望值為:
: : 1*[C4取2] [C7取2]
: : =2/7
: 如果我沒有誤會你的思路的話,
: 這一步邏輯似乎有問題。
我覺得原原po的解法思路沒問題 就"X軸內積"這個說法不好
兩向量OP(x_1, y_1, z_1)和OQ(x_2, y_2, z_2)的內積是
x_1*x_2 + y_1*y_2 + z_1*z_2
因此兩向量內積的期望值
E(OP.OQ) = E(x_1*x_2) + E(y_1*y_2) + E(z_1*z_2)
= 3*E(x_1*x_2) (因為三軸對稱)
而x_1*x_2只有在兩向量x軸分量皆為1時=1 其餘狀況=0
兩向量x軸分量皆為1的機率 = 4*3/7*6 = 2/7 故所求=6/7
: 首先你以x軸為例,
: 就表示以編號1為P,拿OP去和其他向量作內積
: 這時候會和OP內積為1的只有Q在編號2、3、4的位置(題設P =/= Q)
: 也就是只有3種選擇,
: 你用C(4,2)就很奇怪,這時P怎麼能變動?
: 再說O3向量 和 O4向量 的內積是2!不是1!
: 我的作法是除了O和編號3之外,其餘再分成地位相同的兩群
: [0 + (2 + 0) * 3 + 1 * 3 + 2 * 3 + 1 * 3]/C(7, 2)
: = 3 * [2 + 1 + 2 + 1] / 21
: = 18/21 = 6/7
: 雖然就算式而言可以寫成3 * (),
: 但是計數時的地位不一樣,
: 不會貿然直接乘以3
: : 而立方體是三軸對稱,
: : 所以答案就是
: : 2/7+2/7+2/7=6/7
: : 這樣解,
: : 明明就乾淨俐落很多。
: : 只能說數學無捷徑,
: : 還是不要過度依賴chatgpt啊。
我覺得AI沒有不好 我解板上的題目也會先丟ChatGPT試試看
低機率花一分鐘就得到自己想半小時才想到的思路
題外話 最近讀GSLin的部落格看到Stack Overflow的提問數統計
ChatGPT出現後 提問數從每個月87543跌到現在的3862......
https://data.stackexchange.com/stackoverflow/query/1926661#graph
--
▃▅▅▃
◢██◣
▄◢████◣▄
██﹥﹤██
▄ ◥ Ω ◤ ▄
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 118.169.129.161 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1767968416.A.0A5.html
討論串 (同標題文章)
完整討論串 (本文為第 5 之 12 篇):