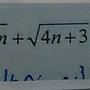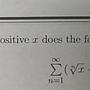Re: [微積] 極限
完整的第二題如下
(為了方便,以下的lim都是lim )
n->無限
題目:設f:(0,無限)->R為一函數,
[x^1/2]
且滿足 0 < f(x) < --------- , for all x > 0
= = x+1
取數列{a_n}
滿足a_n = {(1+f(1))(1+f(2))...(1+f(n))}^1/n ,for all n > 0
=
試求極限 lim a_n .
解答:因為
lim a_n = exp{lim(1/n){ln(1+f(1))+ln(1+f(2))+...+ln(1+f(n))}}
但是
[n^1/2]
0 < f(n) < --------- -> 0 n->無限
= = n+1
故可得
limln(1+f(n)) = 0
所以
lim a_n = 1
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 111.253.11.8
討論串 (同標題文章)