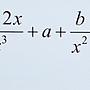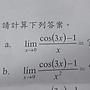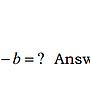Re: [微積] 一題極限
※ 引述《c5ckk (蔡脯)》之銘言:
: lim(x,y)->(0,0) sin(xy)/xy = 1
: lim(x,y,z)->(0,0,0) sin(xyz)/xyz = ?
: 總覺得也是1
: 可是答案給的是0
: 請問要怎麼算??
兩個都是1吧
Define f(x,y) = sin(xy)/(xy) , if x,y =/= 0
1 , if x=0 or y=0
Since lim sinx/x = 1
x→inf
so for e > 0 , there exists 1 > d_e > 0 , (取d_e與1之min即可做到這件事)
s.t. │sinx/x - 1│< e , if 0 <│x│< d_e ------------ (*)
Then for e > 0 , take the same d_e as above
if 0 < (x^2+y^2)^(1/2) < d_e
then :
Case1=> x=0 or y=0 → then f(x,y) = 1 , so │f(x,y) - 1│= 0 < e
Case2=> x,y =/= 0 → Since 0 < (x^2+y^2)^(1/2) < d_e
so 0 <│x│< d_e , 0 <│y│< d_e
hence 0 <│xy│< d_e^2 < d_e (Since d_e < 1)
so │f(x,y) - 1│
= │sin(xy)/(xy) - 1│ < e (from (*))
--------------------------
xyz亦是
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 111.243.156.43
推
11/10 22:18, , 1F
11/10 22:18, 1F
→
11/10 22:18, , 2F
11/10 22:18, 2F
討論串 (同標題文章)