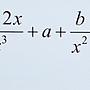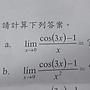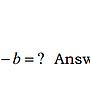[微積] 一題極限

看板Math作者 (.....)時間14年前 (2012/02/02 15:37), 編輯推噓3(3推 0噓 9→)
留言12則, 5人參與, 最新討論串12/37 (看更多)
lim (log2+log3+...+logn)/n n->∞ 我覺得答案應該是0，可是不知道該怎麼下手 -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 114.24.141.223
推
02/02 15:40, , 1F
裡面的東西=(logn!)/n=log(n!)^(1/n) 又n!^(1/n)->1
02/02 15:40, 1F
→
02/02 15:41, , 2F
當n->無窮,利用log function是連續的性質我們可以把
02/02 15:41, 2F
→
02/02 15:41, , 3F
limit搬到log裡面. then done
02/02 15:41, 3F
推
02/02 15:50, , 4F
怪怪的 .. \sum log(k) = Ω(n log n), 不是發散嗎?
02/02 15:50, 4F
→
02/02 15:55, , 5F
發散 用Stolz theormm
02/02 15:55, 5F
→
02/02 15:58, , 6F
對了n!^(1/n)是-infinity喔
02/02 15:58, 6F
→
02/02 15:59, , 7F
(變負的!?)
02/02 15:59, 7F
→
02/02 16:00, , 8F
是+的 不小心把>砍掉
02/02 16:00, 8F
→
02/02 16:01, , 9F
n! >= e*(n/e)^n n!^(1/n) >= e^(1/n) * n/e
02/02 16:01, 9F
推
02/02 16:09, , 10F
Stirling Formula應該也可以用
02/02 16:09, 10F
→
02/02 16:10, , 11F
突然發現就是stimim大的方法XD
02/02 16:10, 11F
→
02/04 14:09, , 12F
sorry 極限那邊搞錯 = =|||
02/04 14:09, 12F
‣ 更多 robert780612 的文章
文章代碼(AID): #1FAZrBa9 (Math)
討論串 (同標題文章)
以下文章回應了本文 (最舊先)：
完整討論串 (本文為第 12 之 37 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共37篇)
‣ 更多 robert780612 的文章
文章代碼(AID): #1FAZrBa9 (Math)