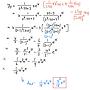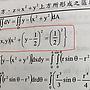作者 max93765 在 PTT [ Math ] 看板的留言(推文), 共39則

[其他] 逆運算求特解

[ Math ]7 留言, 推噓總分: +2

作者: Yic0197 - 發表於 2021/08/04 16:56(4年前)

1^F推max93765: Y大有學過這個性質嗎？08/04 19:42

2^F→max93765: L(D)[f(x)‧e^ax]=e^ax‧L(D+a)[f(x)]08/04 19:42

3^F→max93765: 如果有可以套這個性質去找特解就好08/04 19:43

4^F→max93765: https://i.imgur.com/igj23pX.jpg08/04 19:43

5^F→max93765: 紅色的部分會被併入前面的齊性解08/04 19:43

6^F→max93765: 這樣解答就一樣了08/04 19:43

7^F推max93765: 你說你的作法嗎08/04 19:47

[微積] 三重積分觀念

[ Math ]14 留言, 推噓總分: 0

作者: max93765 - 發表於 2021/06/23 23:08(4年前)

7^F→max93765: 請問一下y大把R變成D是解聯立嗎？06/24 11:00

8^F→max93765: 還有我要如何將上下限換成極座標？06/24 11:00

[其他] 工數-傅立葉cos/sin 級數

[ Math ]8 留言, 推噓總分: +2

作者: max93765 - 發表於 2021/06/17 17:43(4年前)

2^F→max93765: 所以BC只是決定展開的週期函數圖型長怎樣而已嗎？06/18 18:18

6^F→max93765: 壞掉是指斷掉的意思嗎06/19 00:53

8^F→max93765: 瞭解了謝謝06/19 09:05

Re: [其他] 工數傅立葉一題

[ Math ]20 留言, 推噓總分: +4

作者: Honor1984 - 發表於 2021/06/13 23:48(4年前)

20^F推max93765: 有有有我好像比較懂了謝謝你06/17 17:33

1^F推max93765: 為什麼直接積啊我是不太理解題目是x06/14 08:15

2^F→max93765: 然後積分變數是t的意義06/14 08:15

4^F推max93765: X在上下限所以t只是啞變數嗎06/14 23:53

5^F→max93765: 我有點懵06/14 23:53

9^F推max93765: 我不太瞭解啞變數所以f(t)就是f(x)嗎06/15 09:21

10^F→max93765: 那t跟x有關係式嗎06/15 09:21

Re: 工數傅立葉

[ Math ]3 留言, 推噓總分: +1

作者: Honor1984 - 發表於 2021/05/28 17:53(4年前)

1^F推max93765: 哈哈可以解釋一下嗎謝謝05/28 21:05

工數傅立葉

[ Math ]8 留言, 推噓總分: +1

作者: max93765 - 發表於 2021/05/27 23:12(4年前)

4^F→max93765: 那如果今天我x^2改成1 其他條件不變那還可以使用05/28 08:49

5^F→max93765: 帕賽維爾嗎？05/28 08:49

6^F→max93765: 意思是代值進去後就不是積一個函數變積常數了嗎05/28 08:50

[微積] 感到困惑

[ Math ]26 留言, 推噓總分: +2

作者: max93765 - 發表於 2019/05/12 20:25(6年前)

3^F→max93765: 答案是寫第7題不能用微分的除法原則誒05/12 21:16

4^F→max93765: 題目是問有無必要還是適不適用05/12 21:16

8^F→max93765: 這個前提是單變數就有講嗎05/12 21:19

9^F→max93765: 我課本找不到05/12 21:19

13^F→max93765: 哪裡找得到quotient rule 的使用前提？05/12 21:21

16^F→max93765: 那我問一個：如果分子分母任一個沒有自變數就不能05/12 21:33

17^F→max93765: 用quotient rule了嗎05/12 21:33

[微積] 一題vector-valued function

[ Math ]3 留言, 推噓總分: 0

作者: max93765 - 發表於 2019/05/06 11:17(6年前)

2^F→max93765: 不能直接找嗎05/06 12:09

[微積] Taylor’s theorem proof

[ Math ]7 留言, 推噓總分: +2

作者: max93765 - 發表於 2019/04/08 11:57(6年前)

3^F→max93765: 我查過了但我看不太懂04/08 12:32

4^F→max93765: http://www.larsoncalculus.com/calc10/content/pro04/08 12:33

5^F→max93765: of-videos/chapter-9/section-7/proof-taylors-theo04/08 12:33

6^F→max93765: rem/04/08 12:33

7^F→max93765: 影片在這04/08 12:34

[微積] 關於有界單調數列的收斂性

[ Math ]9 留言, 推噓總分: +2

作者: max93765 - 發表於 2019/03/04 18:53(6年前)

3^F→max93765: 沒有下界它還是會收斂吧但它就是一定有下界存在就03/04 19:35

4^F→max93765: 對了嗎03/04 19:35

6^F→max93765: 所有遞減亦然嗎03/04 20:22

作者查詢 / max93765