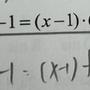Re: [中學] 三題高中數學


: 謝謝大家
※ 引述《chc1984 (這就是暱稱)》之銘言:
: 有三題高中數學有點沒頭緒
: 想請教大家
: 範圍是分科測驗
: https://i.imgur.com/ckaH4os.jpeg


: 謝謝大家
12.
|z-6|/|z+2| = 1/4
設 z = a + bi , a, b為實數
16(a-6)^2 + 16b^2 = (a+2)^2 + b^2
=> 15a^2 - 196a + 572 + 15b^2 = 0
=> (a-98/15)^2 + b^2 = 1024/225
=> z 在 以 98/15 為圓心, 32/15 為半徑 的圓上
又 z-6 與 z+2 的夾角為 0 < 2theta < pi
從圖形可知 z 的可能範圍為整個上半圓不含左右兩端
因此 98/15-32/15 < |z| < 98/15 + 32/15
答案為 22/5 < |z| < 26/3
13.
令 A = -2 , B = 6 , C = z, D=k
則角 BCA = 2theta, 角 DCA = theta
=> CD 為角 BCA 的角平分線
AD: BD = AC:BC = 4:1
更正:
|k+2| = 4|k-6|, -2 < k < 6
=> k+2 = 4(6-k)
=> k = 22/5
角平分線長 CD = 2 AC*BC/(AC+BC) cos(theta)
=> r = CD/AC = 2/5 cos(theta)
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 220.137.16.43 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1720514970.A.8E2.html
※ 編輯: mantour (220.137.16.43 臺灣), 07/09/2024 16:50:09
※ 編輯: mantour (220.137.16.43 臺灣), 07/09/2024 16:51:11
推
07/09 17:29,
1年前
, 1F
07/09 17:29, 1F
※ 編輯: mantour (220.137.16.43 臺灣), 07/09/2024 18:29:46
※ 編輯: mantour (220.137.16.43 臺灣), 07/09/2024 18:30:22
k 列式錯了, 已更正
※ 編輯: mantour (220.137.16.43 臺灣), 07/09/2024 18:35:04
→
07/22 10:40,
1年前
, 2F
07/22 10:40, 2F
討論串 (同標題文章)