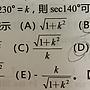[中學] 三角函數

看板Math作者 (類)時間7年前 (2018/05/17 20:10), 編輯推噓3(3推 0噓 6→)
留言9則, 4人參與, 7年前最新討論串198/232 (看更多)
sinx+cosx=根號2 , 求tan(x/2)=? 法1: (sinx+cosx)^2 = (根號2)^2 => sin2x=1 => 2x=2n*Pi+ Pi/2 => x=n*pi + pi/4 =>tan(x)=tan(n*pi + pi/4)=tan(pi/4)=1 => 1= 2t/(1-t^2) t=tan(x/2) => t=-1+根號2 , -1-根號2 法2: t=tan(x/2), 則 2t/(1+t^2) + (1-t^2)/(1+t^2)=根號2 => 整一下 代公式=> t=根號2-1 兩種方法似乎都沒錯 但答案差一個 怎會這樣呢 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 114.38.226.209 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1526559033.A.AA2.html
推
05/17 20:26, 7年前 , 1F
我沒仔細看 目前看是 法2:一元二次式 應該要有兩解
05/17 20:26, 1F
→
05/17 22:27, 7年前 , 2F
回樓上 法二的判別式=0 Q_Q
05/17 22:27, 2F
推
05/18 00:03, 7年前 , 3F
法1有誤, 由 tan x = 1 去算 tan(x/2) 會多一解
05/18 00:03, 3F
→
05/18 00:04, 7年前 , 4F
這兩解分別是 tan(pi/8) 跟 tan(5pi/8)
05/18 00:04, 4F
→
05/18 00:05, 7年前 , 5F
咦等等...我再仔細想想 @@ 好像哪裡怪怪的
05/18 00:05, 5F
→
05/18 00:06, 7年前 , 6F
OK, 應該是這樣沒錯 -- x = 5pi/4 不合原式
05/18 00:06, 6F
推
05/18 00:08, 7年前 , 7F
然後仔細看了看這個增根是增在第一步的兩邊平方
05/18 00:08, 7F
→
05/18 00:09, 7年前 , 8F
而不是到 tan 才有問題...
05/18 00:09, 8F
→
05/18 13:05, 7年前 , 9F
法3 疊合sin(x+π/4)=1, x=2nπ+π/4就不會有5π/4
05/18 13:05, 9F
‣ 更多 kku6768 的文章
文章代碼(AID): #1Q_N4vgY (Math)
討論串 (同標題文章)
完整討論串 (本文為第 198 之 232 篇)：
排序： 最新先 | 最舊先 | 留言數
中學
9
22
[中學] 三角函數 三角函數
hiu
1年前, 02/02
在新視窗開啟完整討論串 (共232篇)
‣ 更多 kku6768 的文章
文章代碼(AID): #1Q_N4vgY (Math)