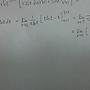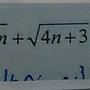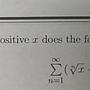Re: [微積] 極限

: 請問大大
: 此題算到這裡
: 極限該如何繼續往下解呢
: 請大大解惑
: 感恩
lim 1 1
(----- - ------)
x-> 0 lnx xlnx
lim 1 y
= (- ----- + -----)
y->∞ lny lny
lim y-1 ∞
= (-------) (----) =>用羅比達定理,上下微分
y->∞ lny ∞
lim 1 lim
= (-----) = y ->∞
y->∞ 1 y->∞
-----
y
=>發散 =>原題的答案為發散
如果要用想的話 就是x的遞增速度會比lnx的遞增速度來的快
所以當x很接近0(1/x很大很大)的時候
1/x*(-lnx)就會趨近於無窮大
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 123.195.2.247
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1435751631.A.9F1.html
※ 編輯: kevin77884 (123.195.2.247), 07/01/2015 20:32:43
推
07/01 21:47, , 1F
07/01 21:47, 1F
討論串 (同標題文章)