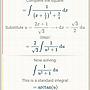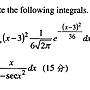[微積] 兩題積分

看板Math作者 (田中鬪莉王)時間13年前 (2012/04/17 04:00), 編輯推噓1(1推 0噓 3→)
留言4則, 1人參與, 最新討論串9/23 (看更多)
1. ∞ e^(-ax) - e^(-bx) b^2 + r^2 試證 ∫ ------------------- dx = 0.5 ㏑ ----------- a, b > 0 0 xsecrx a^2 + r^2 2.試證 ∞ 1 - cosx -1 1 α α ∫ e^(-ax) ----------- dx = tan ─ - ─ ㏑( α^2 + 1 ) + ─ ㏑ α^2 0 x^2 α 2 2 -- "HARD WORK BEATS TALENT WHEN TALENT FAILS TO WORK HARD." -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 140.114.209.10
推
04/17 05:03, , 1F
兩題都可透過引入 ∫e^(-xt)dt (配合適當的上下限)來
04/17 05:03, 1F
→
04/17 05:05, , 2F
吸收分母的x，化為多重積分後利用Fubini定理交換積分
04/17 05:05, 2F
→
04/17 05:06, , 3F
次序，較易求出結果。(第二題答案似乎有誤，應為
04/17 05:06, 3F
→
04/17 05:08, , 4F
arctan(1/a)-(a/2)*ln((1/a)^2+1), a>0 (a即alpha?)
04/17 05:08, 4F
阿 我漏打了 我大概懂意思了，先算算看 感謝您~ m(_ _)m ※ 編輯: tanaka0826 來自: 140.114.209.10 (04/17 18:12)
‣ 更多 tanaka0826 的文章
文章代碼(AID): #1FZ7fOz2 (Math)
討論串 (同標題文章)
完整討論串 (本文為第 9 之 23 篇)：
排序： 最新先 | 最舊先 | 留言數
微積
3
5
[微積] 兩題積分 兩題積分
ksxo
10年前, 11/28
在新視窗開啟完整討論串 (共23篇)
‣ 更多 tanaka0826 的文章
文章代碼(AID): #1FZ7fOz2 (Math)