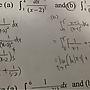[微積] 瑕積分
+∞
令f(x)=1,|x|<a; f(x)=0,|x|>a; 計算∫ f(x)e^iwx dx=?
-∞
解:
-a a +∞
∫ 0*e^iwx dx+∫ 1*e^iwx dx+∫ 0*e^iwx dx
-∞ -a a
|a
= 0 +(1/iw)*e^iwx| +0
|-a
=(1/iw)*(e^iwa-e^iw(-a))
=(1/iw)*(e^(-1))
=(1/iwe)
抱歉,很久沒算數學了,很怕自己寫出一個很好笑的算法@@
不知道這樣解對嗎?
那x=a跟x=-a時怎麼辦?
謝謝~
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 59.124.227.67
推
06/28 12:02, , 1F
06/28 12:02, 1F
→
06/28 23:29, , 2F
06/28 23:29, 2F
推
06/28 23:31, , 3F
06/28 23:31, 3F
討論串 (同標題文章)