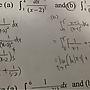Re: [微積] 瑕積分
※ 引述《noyl91 (azure)》之銘言:
: ∫ x^(-1/3) * (x+1)^(-5/3) dx
令u=x^(-1/3)
原積分
= ∫-3[u^3/(1+u^3)]^(5/3) * u^(-3) du
= ∫-3 u^2 /[(1+u^3)]^(5/3) du
= ∫-1/[(1+u^3)]^(5/3) d[1+u^3]
= 3/2 * (1+u^3)^(-2/3)
= 3/2 * [x/(x+1)]^(2/3)
: 3 x
: Ans: --- [-----]^(2/3)
: 2 x+1
: 用過變數代換令 u = x+1,
: 也試過分部積分,
: 但還是算不出來...
: 也想不到有什麼其他的方法可以解 ~"~
: 希望有人可以給個方向,非常謝謝!
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 128.220.212.176
推
06/18 14:38, , 1F
06/18 14:38, 1F
討論串 (同標題文章)