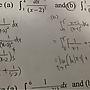[微積] 瑕積分

看板Math作者obelisk0114 (追風箏的孩子)時間14年前 (2011/06/21 01:10)推噓2(2推 0噓 3→)

留言5則, 2人參與討論串5/21 (看更多)

一般瑕積分好像是 +∞ 0 R ∫ f(x)dx = lim ∫ f(x)dx + lim ∫ f(x)dx -∞ r->∞ -r R->∞ 0 利用複數積分所處理的瑕積分是Cauchy's Principal value +∞ r ∫ f(x)dx = lim ∫ f(x)dx -∞ r->∞ -r 兩者之間有差異 ex: +∞ 0 R ∫ xdx = lim ∫ xdx + lim ∫ xdx ->極限不存在 -∞ r->∞ -r R->∞ 0 +∞ r ∫ xdx = lim ∫ xdx = lim (r^2/2-(-r)^2/2) = 0 -∞ r->∞ -r r->∞ 碰到瑕積分時,用複數積分求解的是Cauchy's Principal value 不就和一般瑕積分不相同了? -- │ ███ ▂▄▃ ││││ │ ˋ ◤Mooncat~◥││││ 「為什麼， │ ‵ ◤ ◥▏*_▂▁ ▋ │││ 為什麼教授這麼靠盃 │ ′ 、▌█ ▊▉▏ │ 沒天理啊………」 ◢ ◤◢ ◣▋◢ █ ▋▊ ▕▅▇ ◥◥＊Mooncat~ ◢ ▂▇ˋ█▆◤ ▂_ ▁▄▆▇▃ by mooncats -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 140.112.245.27

推

jacky7987

06/21 01:18, , 1^F

06/21 01:18, 1^F

→

jacky7987

06/21 01:18, , 2^F

06/21 01:18, 2^F

→

jacky7987

06/21 01:18, , 3^F

06/21 01:18, 3^F