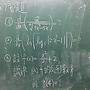Re: [微積] 三題微積分
※ 引述《chribaby (過去˙現在˙未來)》之銘言:
: http://www.lib.ntu.edu.tw/exam/graduate/97/97051.pdf
: 還有這一份的第11題
sin(x)=x-x^3/6+x^5/5!....
sin(x^2)=x^2-x^6/6....
(sin(x))^2=(x-x^3/6+x^5/5!....)(x-x^3/6+x^5/5!....)=x^2-x^4/3....
看起來sin(x^2)比較大
所以目標證明sin(x^2)-(sin(x))^2在(0,1)大於零
求導後得到2x*cos(x^2)-2sin(x)*cos(x)
在(0,1)間, x>sin(x) (半徑是1, 角度是x的扇形, 弧長=x, 高=sin(x))
cos(x^2)>cos(x) (cos遞減, x^2<x)
所以在(0,1)間導數是正的
sin(x^2)-(sin(x))^2在x=0處為零, 在(0,1)間遞增, 所以是正的
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 69.223.185.63
討論串 (同標題文章)