作者查詢 / binbinthink

總覽項目：發文 | 留言 | 暱稱

作者 binbinthink 在 PTT [ Math ] 看板的留言(推文), 共752則

限定看板：Math

看板排序：

全部CS_TEACHER1781tutor770Math752MapleStory194toberich106teaching84HomeTeach78JX375JOB-Hunting61FengYuan39ONE_PIECE39Keelung29marriage25Old-Games24babysitte15AION13PttLifeLaw13job11Salary10maruko8PeopleSeries8part-time7BBSmovie6GetMarry6Hate4Isayama4TuTsau4Food3NCCU_trans3Sony-style3trans_math3Visual_Basic3Benny_Chan2Doraemon2L_LifeJob2scu_transfer2SET2Transfer2wretch2ASHS-93-li1Aviation1B95303XXX1Buddhism1ChungShin3311ck57th3041cksh78th201CMU_M481CMU_M491CSMU-bridge1CSMU-MED931CSMU-MED971CSMU-MIS941CSMU-MT931CSMU-MT941CSMU-MT951CSMU-OT951CSMU-SO1CTSH923011CTSH97EXP1CYCU_BME91B1FamilyCircle1FJU-ACC94b1FJU-Chinese1FJU-Leader1FJU_NIGHT1flying1FXM91-3291Gemini1Haruhi1HisShark1HLHS_10thU1HSNU_10551HTSH913121Instant_Mess1joke1KG94-301.21KG95-3041KS92-3071KS94-3111KS94-3131KS94-3201ME_BADMINTON1Men5431NCCU07_DIP1NCCU07_Math1NCCU_mathG981NCCU_mathG991NCHU-AGR031NCHU-AGR061NCHU-KF1NCHU-photo1NCYU_HoRt_951NCYU_MIS_971NDHU-phy961NDHU-phy981NDHU_ACC_8th1NDHU_ACC_9th1NDMC-guitar1NKNU_OECE971northtrans1NSYSU_EE95-11NTPU-ACC951NTPU-COECO941NTU-EM921NTUBST951NTUDormM71NTUE-ME981NTUE_Nse991NTUF-951NTUMEB951NTUmed911Palmar_Drama1pay_home1pccu_ee891PT-941RIPE_gender1RSSH91_3021RSSH94_3031SCU_chem921sex1SHIAW1SSSH-13th3111TaiwanDrama1TakkiTsubasa1TalesWeaver1TFSHS67th3091TFSHS67th3261THU-CHEM941THU_BA20001TKU_INS1TuCheng1WuLing46-3051YCSH_alumni1YP95-3131Yup02-031Zastrology1<< 收起看板(136)

首頁

尾頁

[中學] 一圓繞著另一圓

[ Math ]2 留言, 推噓總分: +1

作者: snow3804 - 發表於 2015/02/05 20:52(11年前)

1^F→binbinthink: 我算好像是六點...02/05 21:12

[其他] 兩個相同的整數算是連續整數？

[ Math ]4 留言, 推噓總分: +1

作者: egg224488 - 發表於 2015/01/26 11:40(11年前)

1^F→binbinthink: 相同的人一直買咖啡=連續的人一直買咖啡?01/26 13:52

[幾何] 請教一題正三角形的問題

[ Math ]7 留言, 推噓總分: +3

作者: waynan - 發表於 2015/01/21 13:07(11年前)

1^F推binbinthink: 若是Pk1/Oh1 + Pk2/Oh2 + Pk3/Oh3 應該會=301/21 14:34

2^F→binbinthink: 分子分母相反的話,我覺得不像個定值01/21 14:34

[中學] 內心和相似性

[ Math ]3 留言, 推噓總分: +1

作者: hoodlumcrow - 發表於 2015/01/17 11:54(11年前)

1^F推binbinthink: 只需用到內心性質,連BI跟CI01/17 12:35

2^F→binbinthink: 角度標一標可知BIE和CIF皆為等腰三角形01/17 12:36

3^F→binbinthink: BC=BE+EF+FC=IE+EF+FI=1201/17 12:37

[中學]國中題庫

[ Math ]6 留言, 推噓總分: +1

作者: xz35s8pq - 發表於 2015/01/17 11:08(11年前)

1^F→binbinthink: 有地方可以抓各校考古題,那也是種練習,而且可以知道01/17 11:18

2^F→binbinthink: 國中現在都常考些什麼,一舉兩得01/17 11:19

4^F→binbinthink: 我不知道這種資訊能不能PO在這,我寄信給你好了01/17 12:39

Re: [中學] 機率

[ Math ]4 留言, 推噓總分: +3

作者: Honor1984 - 發表於 2015/01/14 15:34(11年前)

1^F推binbinthink: H大,我覺得第(1)題好像......01/14 15:51

2^F推binbinthink: ^^01/14 15:57

3^F推binbinthink: 不客氣,我覺得您超強的,下到國小,上至大學,都能看到01/14 16:02

4^F→binbinthink: 您幫大家解題,衷心的佩服您01/14 16:03

[機統] 高中機率

[ Math ]12 留言, 推噓總分: +2

作者: dinglynn - 發表於 2015/01/12 15:48(11年前)

1^F→binbinthink: 第2題,分勝負有六種情形01/12 15:59

3^F→binbinthink: 甲甲,甲乙甲,乙甲甲(甲贏);乙乙,乙甲乙,甲乙乙(乙贏01/12 16:00

6^F→binbinthink: 3/4*3/4 + 3/4*1/4*3/4 + 1/4*3/4*1/4 = 54/6401/12 16:01

8^F→binbinthink: 是呀,我只是說明呀,列式的地方只有甲贏沒錯呀01/12 16:02

11^F→binbinthink: 1/4*3/4*3/4<==第三項錯了01/12 16:12

[中學]幾題競賽題目求解

[ Math ]8 留言, 推噓總分: 0

作者: zp5000 - 發表於 2015/01/08 14:16(11年前)

1^F→binbinthink: 21題,三角形AMB相似於三角形NMD,MN:AM=DM:BM01/08 14:27

2^F→binbinthink: 三角形ADM相似於三角形PBM,DM:BM=AM:PM01/08 14:28

3^F→binbinthink: 2:AM=AM:8,AM=4Y01/08 14:28

4^F→binbinthink: Y自己跑出來的,沒有Y01/08 14:28

5^F→binbinthink: 26題,延長射線DP交圓O於C',可利用ASA證明PC=PC'01/08 14:35

6^F→binbinthink: PC*PD=PC'*PD=PA*PB(內冪)=7*13=9101/08 14:35

7^F→binbinthink: (證ASA時需要用到AB為直徑這件事喔!!!)01/08 14:38

8^F→binbinthink: 25題我的算法太長啦,我回篇文比較方便喔,抱歉01/08 14:45

[中學] 高一數列級數

[ Math ]14 留言, 推噓總分: +1

作者: allen01906 - 發表於 2015/01/03 15:47(11年前)

1^F→binbinthink: 你把S1列三項,T1也列三項,帶進去關係式中,證證看01/03 15:52

2^F→binbinthink: 你就會懂了01/03 15:53

3^F→binbinthink: a1...(a1+a2)...(a1+a2+a3)01/03 15:54

4^F→binbinthink: b1...(b1+b2)...(b1+b2+b3)01/03 15:54

6^F推binbinthink: S1=a1,T1=b1先帶入S1:T1=(3*1+2):(7*1+5)01/03 17:08

7^F→binbinthink: 得a1:b1=5:12,設a1=5k.....b1=12k01/03 17:09

8^F→binbinthink: 然後再設a2=5k+P.....a3=5k+2P <===等差的設法01/03 17:09

9^F→binbinthink: b2=12k+Q.....b3=12k+2Q01/03 17:10

10^F→binbinthink: 然後再利用S2:T2的關係式和S3:T3的關係式,01/03 17:11

11^F→binbinthink: 得到兩方程式(k..P..Q三未知數)01/03 17:11

12^F→binbinthink: 將P與Q分別消去,會得到P=多少k和Q=多少k01/03 17:12

13^F→binbinthink: 再把P.Q都帶回等差假設那邊,就可得每一項01/03 17:12

[中學] 重心的題目

[ Math ]12 留言, 推噓總分: +2

作者: justin0602 - 發表於 2015/01/02 20:19(11年前)

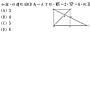
2^F推binbinthink: 直線CE與直線AD交於某點,接下來是相似01/02 21:14

3^F→binbinthink: 先作作看,加油,真作不出,我再打詳解01/02 21:15

6^F→binbinthink: 應該要平行四邊形01/03 09:03

首頁

尾頁