看板
[ Math ]
討論串[中學] 兩題中學數學 (國三)
共 5 篇文章
內容預覽:
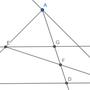
AD 跟 EC 交點為 P. 角 AEC = 角 BAD. 角DAC = pi/2 - 角BAD = pi/2 - 角AEC = 角ACE. => PE=PE=PC. => 三角形APB面積 = 1/2 三角形ABC面積 = 三角形APC面積+三角形APC面積. AE=EB. => 三角形APC面積
(還有111個字)
內容預覽:
(1) 圓是三角型ABH的內切圓,所以表示圓心O到A點的連線AO是角BAH的角平分線. (2) 又,角CMB=角AMP,所以角MCB=(角MAP)/2. (3) 由(1)與(2),線CP正交於線AO. (4) 由(3),所以三角形AMP被AO分為兩個全等三角型. (5) 由(4),所以三角形AMO全
(還有77個字)
內容預覽:
我想到另一個做法. 設AD交EC於F 因為∠AEC=∠EAD => AF = EF. 又∠FAC = 直角 - ∠EAD = ∠ACF => AF = CF. 所以EF = CF. 做通過E點,平行BC的直線,交AD於G點. https://i.imgur.com/Y3IEiKt.jpeg. 有△E
(還有403個字)
內容預覽:
你這兩題的思考方向都錯!. BC中點J,令BC = 2R. 1/2 = (R - 7)/7 => R = 21/2. => BC = 21. AH = 8,BH = 6,AB = 10 => AP = 6. => △APC = (6/10) * (1/2) * 8 * 12 = 144/5. --.
(還有17個字)
內容預覽:
1.∠BAC為直角 E為AB中點 ∠AEC=∠BAD CD=7 求BC=?. https://i.meee.com.tw/56AHezO.png. 交點應該是外心 不過暫時沒想到往下一步算法. 2.△ABC是等腰 AB=AC=10 BC=12 AH與BC垂直. △ABH之內切圓與AH交於M CM交A
(還有155個字)