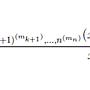Re: [分析] Hermite內插演算法的證明

看板Math作者LimSinE (r=e^theta)時間8月前 (2023/08/19 21:47)推噓3(3推 0噓 11→)

留言14則, 2人參與討論串5/6 (看更多)

Lemma 1: 設f 在a點k+1次可微分，則必在a附近k次可微分設g(x) = (f(x)-f(a))/(x-a) if x=/=a, g(a)=f'(a) 則有 (1) g 在a附近k次可微分，且g^(k)在a點連續 (2) g^(k)(x) =k!{f(a)-[f(x)+f'(x)(a-x)+f"(x)(a-x)^2/2!+...+f^(k)(x)/k!}/(a-x)^(k+1) if x=/=a (3) g^(k)(a)=lim(x->a) g^(k)(x) =f^(k+1)(a) / (k+a) Proof：顯然(2)(3)=>(1) (2)由數學歸納法硬算 (3)的極限求值，把f(x)、f'(x)、f"(x)、...f^(k)(x)全部對x=a做泰勒展開，展到出現f^(k+1)(a)項為止(即f^(s)(x)在a為k+1-s次可微分，展到(k+1-s)階) 所得的餘項雖然不能積分型微分型都不能用，但反正/(a-x)^(k+1)以後會→0 最後 g^(k)(a)=lim(x-a) g^(k)(x) k>0時利用小性質，「若函數在a點連續且附近可微分，極限存在，則在a點可微分，且微分等於極限值。」請相信上述步驟真的可以算XD 有了Lemma 1以後，就可以分析差商(divided difference)了，注意以下差商記號，都假設「所有元素相異」。先引用差商均值定理 Lemma 2: 若 F 在區間I上k次可微分，a0,a1,...,ak屬於I則存在z屬於I使得 F[a0,a1,a2,...,ak] = F^(k)(z)/k! 由此推得 Theorem 1: (1) 設f 在a點k次可微分則 lim(a1,...,ak->a,a,...,a) f[a,a1,...,ak] = f^(k) (a) / k! (2) 設f 在a點附近k次可微分，且f^(k)在a點連續，則 lim(a0,a1,....,ak->a,a,...,a) f[a0,a1,...,ak] = f^(k) (a) / k! proof: (1)觀察到 f[a,a1,...,ak]=g[a1,....,ak] 由Lemma 1，套用差商均值定理得 = g^(k-1)(z)/(k-1)! -> g^(k-1)(a)/k! = f^(k) (a) / k! as z-> a (2) 直接套用差商均值定理得 f[a0,...,ak]= f^(k) (z)/k! -> f^(k)(a)/k! as z->a 結論：差商取極限，對於f比較差的情形(如(1))，必須有一個點固定對於f比較好的情形(如(2))，則所有的點都可以自由移動接下來考慮趨近不同點的情形 Theorem 2. 設有a[1], a[2],...,a[s] 相異點對於i=1,2,...,s, 有a[i][0],a[i][1],...,a[i][k(i)] 共k(i)+1 個點 → a[i] f之條件：對於i=1,...,s 或者(A) f在a[i]點k(i)次可微分，但a[i][0]恆等於a[i] 或者(B) f在a[i]點附近k(i)次可微分，且f^(k(i))在a[i]點連續則 lim f[全部的a[i][j]] = Simga(i=1至s) (d/dt)^(k(i)) {f(t)/Pi(t)}/(k(i)! | t=a[i] 其中 Pi(t) = Product (i'=/=i) (t-a[i'])^(k(i')+1) Proof: 記pi(t) = Product(i'=/=i) Product(j=0至k(i') (t-a[i'][j]) hi(t)=1/pi(t) 則 f[全部的a[i][j]] = Sigma(i=1至s) (f*hi)[a[i][0],a[i][1],...,a[i][k(i)]] 觀察第i項若f 在a[i]滿足(A)則第i項 = gi^(k(i)-1)(z)/(k(i)-1)!, z在a[i]附近其中 gi(t)= (f(t)hi(t)-f(a[i])hi(a[i]))/(t-a[i]) = hi(t) {(f(t)-f(a[i]))/(t-a[i])} - {(hi(t)-hi(a[i]))/(t-a[i])} * f(a[i]) ‧hi(t)、(hi(t)-hi(a[i]))/(t-a[i]) 在a[i]都是很好的有理函數各階微分均一致收斂至 1/Pi(t)、 (1/Pi(t)-1/Pi(a[i])/(t-a[i])之各階微分 ‧由Lemma 1 記Gi(t) = (f(t)-f(a[i]))/(t-a[i]) 則 Gi^(k')(z) ->Gi^(k')(a[i]) for k'<=k-1 故整體→ (d/dt)^(k(i)-1) {f(t)/Pi(t) - f(a[i])/Pi(a[i]))/(t-a[i])}/(k(i)-1)! | t=a[i] 再用一次Lemma 1 = (d/dt)^(k(i)) {f(t)/Pi(t)}/k(i)! | t=a[i] 若f 在a[i]滿足(B)則第i項 = (d/dt)^(k(i)) {f(t)/pi(t)}/k(i)! | t=z 這次僅使用在a[i]附近 1/pi(t)之各階微分一致收斂至1/Pi(t)，即得 → (d/dt)^(k(i)) {f(t)/Pi(t)}/k(i)! | t=a[i] 終於進入插值多項式了設 p(x) = Product(所有a[i][j]) (x-a[i][j]) q(x,t)= (p(t)-p(x))/(t-x) as polynomials 則f 在所有a[i][j]之插值多項式= (fq)[所有a[i][j]] (注意此為x之多項式) 注意到 q(x,t)之各階微分一致收斂至Q(x,t)=P(x)-P(t)/(x-t)之各階微分 P(x)=Product(i=1至s) (x-a[i])^(k(i)+1) Corollary: 插值多項式之極限 F(x) = Simga(i=1至s) (@/@t)^(k(i)) {f(t)Q(x,t)/Pi(t)}/(k(i)! | t=a[i] 其各階微分 F^(r)(x) = Simga(i=1至s) (@/@t)^(k(i)) (@/@x)^(r) {f(t)Q(x,t)/Pi(t)}/(k(i)! | t=a[i] 從這裡終於可以推出插值多項式的極限真的滿足預期插值高階微分的性質 Theorem: F^(r)(a[i])=f^(r)(a[i]) for r<=k(i) Proof: 因 P(t)=(x-a[i])^(k(i)+1)Pi(t)，故 Q(x,t)/Pi(t) = (x-a[i])^(k(i)+1){(Pi(x)-Pi(t))/(x-t)} /Pi(t) + {(x-a[i])^(k(i)+1) - (t-a[i])^(k(i)+1) /(x-t)} 由此可知Q(x,t)/Pi(t) 在x,t=a[i],a[i]之泰勒展開，(x-a[i])^r(t-a[i])^r'係數 1,若r+r'=k(i) 0,若 r+r'=/=k(i)但 r<=k(i) 從這裡就可以算得出來XD -- 中最連緊閉開值大通緻集集在最到映返返中小連緊閉開間值通緻集集。，。，；， -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 219.85.28.155 (臺灣) ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1692452861.A.B6C.html

推

znmkhxrw

08/20 22:22, 8月前 , 1^F

08/20 22:22, 1^F

→

znmkhxrw

08/20 22:22, 8月前 , 2^F

08/20 22:22, 2^F

→

znmkhxrw

08/20 22:22, 8月前 , 3^F

08/20 22:22, 3^F