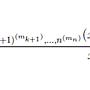看板
[ Math ]
討論串[分析] Hermite內插演算法的證明
共 6 篇文章
內容預覽:
提供另一種證法,. 已知 存在唯一的插值多項式 和 不同插值條件 插值多項式的首項係數,. 證明會符合條件。. 定理.  ̄ ̄. 設 x_0, x_1,..., x_n 為 [a,b] 區間中 n+1 個不同的點,. m_i 為 x_i 重複出現的次數(正整數),N = Σ_{k=0到n} m_k,.
(還有5930個字)
內容預覽:
Lemma 1:. 設f 在a點k+1次可微分,則必在a附近k次可微分. 設g(x) = (f(x)-f(a))/(x-a) if x=/=a, g(a)=f'(a). 則有. (1) g 在a附近k次可微分,且g^(k)在a點連續. (2) g^(k)(x). =k!{f(a)-[f(x)+f'(
(還有3129個字)
內容預覽:
既然你只是要知道爲什麼degeneration law長那樣的話.... ---------------------------------------------------------------. Let F be a field of characteristic 0, a_1,...,a_
(還有2998個字)
內容預覽:
原文吃光光, 這裡舉個wiki的例子. https://en.wikipedia.org/wiki/Hermite_interpolation#General_case. 求滿足 p(-1)=2, p'(-1)=-8, p''(-1)=56. p(0) =1, p'(0) = 0, p''(0) =
(還有1161個字)
內容預覽:
符號看得有點花……. 如果你想做的是「在 x_1 和 x_2 分別趨近 x_0 後所得的極限 = Taylor 多項式」,. 那你需要的就是 MVT of divided differences。. https://en.wikipedia.org/wiki/Mean_value_theorem_(
(還有24806個字)