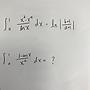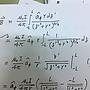[微積] 積分問題

看板Math作者 (open將真的很可愛)時間3年前 (2022/02/24 18:52), 編輯推噓5(5推 0噓 5→)
留言10則, 4人參與, 3年前最新討論串72/74 (看更多)
題目:設f(x)是[a,b]的非負可積分函數， b 若有∫f(x)dx=0，試證明對任給ε>0，存在子區間[α,β]包含在[a,b]， a 使得f(x)<ε，α≦x≦β proof: 假設 存在ε>0，且存在子區間[α,β]包含在[a,b]使得f(x)>ε，α≦x≦β ∵f(x)>ε，α≦x≦β β β ∴∫f(x)dx>∫εdx=ε(β-α) α α ∵f(x)≧0，對所有x屬於[a,b] b α β b ∴ ∫f(x)dx = ∫f(x)dx + ∫f(x)dx + ∫f(x)dx ≧ε(β-α)>0 (矛盾) a a α β 證明完畢。 我沒有很肯定我的寫法有沒有錯誤，請大家指教，謝謝 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 163.20.246.224 (臺灣) ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1645699938.A.5ED.html
推
02/24 19:07, 3年前 , 1F
your proof is wrong due to the wrong contradicti
02/24 19:07, 1F
→
02/24 19:07, 3年前 , 2F
ve statement of conclusion in your asumption.
02/24 19:07, 2F
推
02/24 19:22, 3年前 , 3F
and there is an counterexample as follows: let f
02/24 19:22, 3F
→
02/24 19:22, 3年前 , 4F
be defined on the unit closed interval and be o
02/24 19:22, 4F
→
02/24 19:22, 3年前 , 5F
ne at the rational number and zero others.
02/24 19:22, 5F
推
02/24 19:31, 3年前 , 6F
樓上的例子是勒貝格可積，但黎曼不可積
02/24 19:31, 6F
推
02/24 23:52, 3年前 , 7F
我想一樓的意思是他反證法用的假設有問題吧
02/24 23:52, 7F
推
02/24 23:55, 3年前 , 8F
她這個函數的可積分是定義在什麼積分上啊？
02/24 23:55, 8F
→
02/24 23:55, 3年前 , 9F
Lebesgue ? Riemann ?
02/24 23:55, 9F
→
02/25 10:44, 3年前 , 10F
這邊內容是黎曼可積分，謝謝各位
02/25 10:44, 10F
‣ 更多 OSGrup 的文章
文章代碼(AID): #1Y5sDYNj (Math)
討論串 (同標題文章)
以下文章回應了本文：
完整討論串 (本文為第 72 之 74 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共74篇)
‣ 更多 OSGrup 的文章
文章代碼(AID): #1Y5sDYNj (Math)