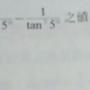Re: [中學] 一題三角函數已刪文
※ 引述《holgaga (Ice)》之銘言:
: ※ 引述《ntuhtking (ㄏㄏ)》之銘言:
: : 有一△ABC滿足2 cos A sin C=sin B的條件,則△ABC的形狀為
: : (A) 正三角形 (B) 直角三角形 (C) 銳角三角形 (D) 等腰三角形 (E) 鈍角三角形
: : 答案:D
: : 出處:北一女
: : 有試過兩邊平方爆開,可是整理不出甚麼結果
: : 對於畫圖沒甚麼sense,想請問這題該如何下筆...
: A+B+C=π B=π-(A+C)
: 2 cos A sin C =sin B
: =sin [π-(A+C)]
: =sin (A+C)
: =sinA cosC + cosA sinC
: cosA sinC=sinA cosC (同除cosA cosC)
: tanA =tanC
: 又 0<A、C<π
: 故A=C
: 為等腰Δ
參考
陳一理
所編著的"三角"
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.58.103.35 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1560737625.A.656.html
討論串 (同標題文章)