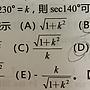Re: [中學] 三角函數已刪文
※ 引述《fir0857 (典)》之銘言:
: arctan(1/(1+x+x^2))=arctan(x+1)-arctan(x)
: 詳解是這樣處理
: arctan(1/(1+x+x^2))=arctan((1+x-x)/(1+(1+x)*x) 接著就變成最後的式子
: 因為根本不知道arctan有甚麼性質 所以根本無從下手 請高手解釋一下 感激
參考
陳一理
所編著的"三角"
假設
gamma=arctan[1/(1+x+x^2)],alpha=arctan(x+1),beta=arctan(x)
於是乎
tan(gamma)=1/(1+x+x^2),tan(alpha)=x+1,tan(beta)=x
tan(alpha-beta)
=[tan(alpha)-tan(beta)]/[1+tan(alpha)tan(beta)]=1/(1+x+x^2)=tan(gamma)
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.58.103.35
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1551720767.A.71A.html
討論串 (同標題文章)