Re: [中學] 內心與垂心共圓

看板Math作者LPH66 (J∪$т М㎝iκä)時間7年前 (2018/10/11 20:01)推噓4(4推 0噓 5→)

留言9則, 5人參與討論串2/3 (看更多)

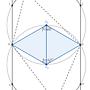
※ 引述《alexan (冷藍)》之銘言： : 已知平面上的線段AB,令C是平面上使得ABC為銳角三角形的一動點， : 設點H為ABC的垂心，點I為ABC的內心。 : 若A.B.H.I四點共圓，求動點C的移動軌跡，及ABC的重心軌跡。由內心性質, ∠AIB = 180 - (1/2)∠A - (1/2)∠B = 90 + (1/2)∠C 由垂心性質, ∠AHB = 180 - (90 - ∠A) - (90 - ∠B) = 180 - ∠C 由 A B H I 共圓知此兩角相等, 可求得 ∠C = 60 度易知所求 C 點軌跡是下圖的兩段實線圓弧 (不含端點): https://i.imgur.com/qQttVHM.png

(這圖裡還有另一個有趣點: 當 C 點在上圓弧時, ABHI 圓是下圓, 反之亦然) ABC 軌跡可以由此求得, 是上面的圓弧往 AB 中點縮成 1/3 而得的(兩段)圓弧 -- 'Oh, Harry, don't you see?' Hermione breathed. 'If she could have done one thing to make absolutely sure that every single person in this school will read your interview, it was banning it!' ---'Harry Potter and the order of the phoenix', P513 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 140.112.30.32 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1539259261.A.EAD.html

推

yyc2008

10/11 21:21, 7年前 , 1^F

10/11 21:21, 1^F

→

Ricestone

10/11 21:32, 7年前 , 2^F

10/11 21:32, 2^F

→

LPH66

10/11 22:05, 7年前 , 3^F

10/11 22:05, 3^F