Re: [中學] 內心與垂心共圓

看板Math作者 (惠雯給我看比基尼)時間7年前 (2018/10/13 21:28), 7年前編輯推噓0(0推 0噓 2→)
留言2則, 1人參與, 7年前最新討論串3/3 (看更多)
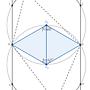
※ 引述《LPH66 (J∪$т М㎝iκä)》之銘言： : ※ 引述《alexan (冷藍)》之銘言： : : 已知平面上的線段AB,令C是平面上使得ABC為銳角三角形的一動點， : : 設點H為ABC的垂心，點I為ABC的內心。 : : 若A.B.H.I四點共圓，求動點C的移動軌跡，及ABC的重心軌跡。 : 由內心性質, ∠AIB = 180 - (1/2)∠A - (1/2)∠B = 90 + (1/2)∠C : 由垂心性質, ∠AHB = 180 - (90 - ∠A) - (90 - ∠B) = 180 - ∠C : 由 A B H I 共圓知此兩角相等, 可求得 ∠C = 60 度 : 易知所求 C 點軌跡是下圖的兩段實線圓弧 (不含端點): : https://i.imgur.com/qQttVHM.png
: (這圖裡還有另一個有趣點: 當 C 點在上圓弧時, ABHI 圓是下圓, 反之亦然) : ABC 軌跡可以由此求得, 是上面的圓弧往 AB 中點縮成 1/3 而得的(兩段)圓弧 參考 九章出版 "初幾研究" 可知 角HAB=pi-C,角IAB=(pi+C)/2 求得C=pi/3 當中ch4的定理6 對已知線段AB的視角等於定角pi/3的 C點軌跡是以AB為弦, 圓周角為pi/3的兩段"弓形弧". -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.58.103.35 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1539437322.A.A4D.html ※ 編輯: wayne2011 (61.58.103.35), 10/14/2018 11:37:26 ※ 編輯: wayne2011 (61.58.103.35), 10/14/2018 16:10:10
→
10/14 16:50, 7年前 , 1F
倒數1st寫出來可能有點問題,大概"圓周角"還是2pi/3.
10/14 16:50, 1F
→
10/15 09:55, 7年前 , 2F
不好意思~沒看到範圍~定角alpha是介於0到pi之間~orz
10/15 09:55, 2F
‣ 更多 wayne2011 的文章
文章代碼(AID): #1RmVCAfD (Math)
‣ 更多 wayne2011 的文章
文章代碼(AID): #1RmVCAfD (Math)