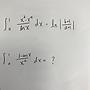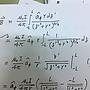Re: [微積] 積分問題
※ 引述《kero961240 (阿哲)》之銘言:
: If f is a quadratic function(i.e. f(x)=Ax平方+Bx+C) such that f(0)=1
: and the indefinite integral 積分f(x)/x平方*(x+1)三次方 dx is a rational
: function, find the value of f'(0) .
: 來源:98交大財金所
: 請問這題該如何解 我看解答始終看不懂 麻煩各位高手了
1. C = 1 , f'(0) = B
f(x) A B 1
2. -------------- = ---------- + ---------- + -------------
x^2 (x+1)^3 (x+1)^3 x(x+1)^3 x^2(x+1)^3
A+1-B B-3 3-B 1 2-B
= ---------- + ----- + ------- + ----- + ---------
(x+1)^3 x (x+1) x^2 (x+1)^2
3. 要讓其不定積分為 rational function,則 B-3 = 0 且 3-B = 0
所以 B = 3
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 114.46.204.71
※ 文章網址: http://www.ptt.cc/bbs/Math/M.1410938489.A.FE6.html
※ 編輯: Eliphalet (114.46.204.71), 09/17/2014 15:49:02
推
09/17 16:16, , 1F
09/17 16:16, 1F
→
09/17 16:16, , 2F
09/17 16:16, 2F
→
09/17 16:23, , 3F
09/17 16:23, 3F
→
09/17 16:24, , 4F
09/17 16:24, 4F
討論串 (同標題文章)