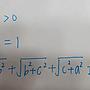[中學] 求最小值
題目: 已知一開口向上的拋物線其圖形與x軸分別交於A(-1,0)、B(t,0)兩點
與y軸交於C點,且過D(1,-2),求△ABC面積的最小值。
以下是我解到一半的解法
設拋物線方程式為y=a(x+1)(x-t), a>0
代入D(1,-2)得a=-1/(1-t) , t>1
x=0代入方程式得C點坐標為(0,t/(1-t))
△ABC面積=1/2.(t+1).(t/(t-1))
=1/2.(t^2+t)/(t-1)
我想請問接下來如何求最小值?
或改成其他解法?
謝謝大家幫忙!
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 1.163.200.86
※ 文章網址: http://www.ptt.cc/bbs/Math/M.1404268671.A.24B.html
推
07/02 11:05, , 1F
07/02 11:05, 1F
推
07/02 11:09, , 2F
07/02 11:09, 2F
→
07/02 11:12, , 3F
07/02 11:12, 3F
討論串 (同標題文章)