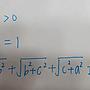Re: [中學] 求最小值已刪文
※ 引述《wayne2011 (婉珊沒有賣比基尼 )》之銘言:
: ※ 引述《susiseptem (..)》之銘言:
: : x,y為實數
: : x^2+y^2-2x+2y-2=0
: : (x-5)^2+(y-2)^2 的最小值
: : 300P答謝
: : 感恩
: 參考
: 陳一理
: 所編著的"圓與球面"
: C':(x-1)^2+(y+1)^2=2^2
: x=1+2cost,y=-1+2sint
: 原式
: =2^2(cost-2)^2+(2sint-3)^2
: =4(cos^2t-4cost+4)+(4sin^2t-12sint+9) = 29-4(4cost+3sint) >= 9 = 3^2 ... ans
亦可參考
九章出版
"解幾學"辭典
可知B(3,-1)在圓C'時 , 鏡射點A'(2,2)有最小值9 .
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.58.103.35 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1567654957.A.BB4.html
※ 編輯: wayne2011 (61.58.103.35 臺灣), 09/05/2019 11:46:13
→
09/05 20:49,
6年前
, 1F
09/05 20:49, 1F
※ 編輯: wayne2011 (61.58.103.35 臺灣), 09/05/2019 20:53:02
討論串 (同標題文章)