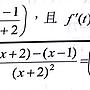[微積] 微分

看板Math作者 (小白)時間12年前 (2013/09/05 15:17), 編輯推噓3(3推 0噓 4→)
留言7則, 3人參與, 最新討論串16/27 (看更多)
假設F為X的函數F(X) 則F對X的ㄧ階微分為dF/dX 然而dF/dX的起源應該要用最原始的微分定義取極限來求： lim deltaX->0[F(X+deltaX)-F(X)/deltaX] 但是很多應用學科只是將兩個微小變量dF&dX相除就說這是微分了 到底這說法有沒有問題？ 是否只要F為X之函數 且X處處連續且可微 這種說法就永遠不會產生問題呢？ 還有ㄧ些人也會這樣表達 將F的變量dF表示為 dF=(dF/dX)*dX 是不是只要F連續且可微 其微分存在就ㄧ定是對的呢？ -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 101.9.253.13
推
09/05 16:09, , 1F
那個是用差分代替微分 因為電腦沒有無限小的數字
09/05 16:09, 1F
→
09/05 16:10, , 2F
他們中間的差異最大可以用二次微分(如果存在且連續的
09/05 16:10, 2F
→
09/05 16:10, , 3F
話)的最大值來估計
09/05 16:10, 3F
推
09/05 21:27, , 4F
dF 就是代表 F 的變化量了 而且是要有多小就有多小
09/05 21:27, 4F
→
09/05 21:28, , 5F
其數學意義就是 limit Δx → 0 的 ΔF
09/05 21:28, 5F
推
09/06 12:45, , 6F
後面那個式子有點冗餘,可看成是偏微分鍊索率的特例
09/06 12:45, 6F
→
09/06 12:47, , 7F
j大講的是寫程式運算的部分,差分也同樣是偏微來的~
09/06 12:47, 7F
‣ 更多 shoesmaster 的文章
文章代碼(AID): #1IA2_liy (Math)
討論串 (同標題文章)
以下文章回應了本文：
完整討論串 (本文為第 16 之 27 篇)：
排序： 最新先 | 最舊先 | 留言數
微積
1
6
[微積] 微分 微分
Keyouka
7年前, 11/03
微積
0
1
[微積] 微分 微分
semmy214
7年前, 05/15
微積
2
5
[微積] 微分 微分
zrush60229
8年前, 10/08
微積
0
3
[微積] 微分 微分
djljing
9年前, 04/14
微積
[微積] 微分 微分
abc0229
10年前, 05/06
微積
1
3
[微積] 微分 微分
xy210742
11年前, 01/19
微積
0
1
[微積] 微分 微分
redwing119
12年前, 12/04
微積
8
34
[微積] 微分 微分
kororoDX
12年前, 10/29
在新視窗開啟完整討論串 (共27篇)
‣ 更多 shoesmaster 的文章
文章代碼(AID): #1IA2_liy (Math)