Re: [中學] 幾何題
※ 引述《Sfly (topos)》之銘言:
: ※ 引述《jetzake (加菲貓)》之銘言:
: : ^^^^^^^^^^^^^^^^^^
: : ^^^^
: : 誠然善哉
: : 我再回一篇... 這次照oldblackwang大人的說法修改題目
: : 應該就可以解的漂亮了 = =+
: : Q:一 △ABC, AB=12, AC=8
: : 有一點 D 在三角形ABC內部 s.t. ∠ADB = 90度 且 ∠ABD = ∠ ACD
: : M 為 BC 中點, 求 DM 長度 = ?
: : ...先說結論 DM長度是2√5
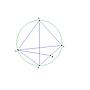
: 做ADB的外接圓 O 與ACD的外接圓 O'
: ∠ABD = ∠ ACD ==> 圓O 與圓O'全等.
: 設M'為AC中點, 則△AO'M'=△ODM (SAS) ==> DM=O'M'=√(6^2-4^2).
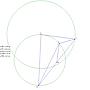
這題我用geogebra圖畫出來 D在三角形外有一解 j大的圖好像忽略了
三角形外的解D'和D對稱於BC中點M 所以MD=MD'
前面各大大的證明也可以適用於D'
不過如果要同時證明 D和D'的話
連AD' CD' 可以證得 D就是三角形 AD'C 的垂心
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 180.177.104.7
推
06/08 21:26, , 1F
06/08 21:26, 1F
→
06/08 21:27, , 2F
06/08 21:27, 2F

→
06/08 21:28, , 3F
06/08 21:28, 3F
→
06/08 21:40, , 4F
06/08 21:40, 4F
那張圖不是限定了 ACB=90度 ?
我看前面的討論是說原PO一開始打錯題目
後來經過更正 (最先題目是打錯什麼我沒看到)
上面那張圖限定了ACB=90度 看起來是無限多解沒錯
如果沒有限定ACB=90度 一般情形下的正常解是兩個
(角ABD=ACD一般情形下D點軌跡是雙曲線 和AB為直徑的圓有四個交點
其中兩個是頂點 A B)
※ 編輯: id010406 來自: 180.177.104.7 (06/08 22:24)
→
06/09 00:23, , 5F
06/09 00:23, 5F
→
06/09 00:24, , 6F
06/09 00:24, 6F
→
06/09 00:25, , 7F
06/09 00:25, 7F
→
06/09 00:27, , 8F
06/09 00:27, 8F
Anyway 我只是想說正好有 D是 AD'C的垂心這個性質
其實如果三角形內有一解 那麼三角形外就必定有一解
用繪圖軟體繪完圖很容易猜到D是垂心 接下來做法就很直接了
※ 編輯: id010406 來自: 180.177.104.7 (06/10 08:41)
→
06/12 03:28, , 9F
06/12 03:28, 9F
討論串 (同標題文章)