Re: [中學] 幾何題
※ 引述《Jinno (TJ)》之銘言:
: 一 △ABC, AB=12, BC=8
: 有一點 D s.t. ∠ADB = 90度 且 ∠ABD = ∠ ACD
: M 為 BC 中點, 求 DM 長度 = ?
: (不好意思, 第一次發問, 還不太懂得怎樣排版最好, 請多多指教! )
: 推 oldblackwang:題目應該少了"D點在三角形ABC內部"的條件 05/24 16:44
^^^^^^^^^^^^^^^^^^
: ※ 編輯: jetzake 來自: 114.36.200.16 (05/25 02:19)
: 推 oldblackwang:圖形不是固定的,正如你說的移動C點會找到符合的D點 05/25 13:19
: → oldblackwang:啊!!我發現題目錯了,是AC=8才對 05/25 13:21
^^^^
誠然善哉
我再回一篇... 這次照oldblackwang大人的說法修改題目
應該就可以解的漂亮了 = =+
Q:一 △ABC, AB=12, AC=8
有一點 D 在三角形ABC內部 s.t. ∠ADB = 90度 且 ∠ABD = ∠ ACD
M 為 BC 中點, 求 DM 長度 = ?
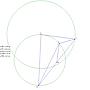
...先說結論 DM長度是2√5
附上圖片... (*長度標示是用GSP的功能 不會出現根號這樣)
http://i.imgur.com/TG0Hd.png


可以看到 確實可以找出來D點 而且任意移動C點時DM長度不變...
這題最大的陷阱就在於 D點其實是用M點去找的..
只要在BC的中點M上 對AC做垂直線 交"以AB為直徑做的圓"的那點就是D
連接AB的中點(設其為"O")和M點 可得 OM =4 (OM=(1/2)AC)
連接OD 可得 OD = 6(OD=(1/2)AB)
再加上∠OMD=90度(DM垂直AC、OM平行AC) DM長度就出來啦...
=============
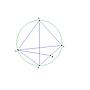
http://i.imgur.com/0bWZj.png


如果照原來的題目來寫 (也就是用"BC=8"的條件) 就會變成這樣
兩張圖片比對一下就知道 移動C點的時候 DM長度會變 所以....= =A
(也是因為計算DM長度會需要用到"(1/2)AC"這個數據的關係...)
=============
...總之 先這樣吧??
詳細的證明我還在整理 弄好了再PO上來
或是哪位板上的大哥願意代勞??
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 114.24.22.72
推
05/25 21:57, , 1F
05/25 21:57, 1F
推
05/25 22:03, , 2F
05/25 22:03, 2F
推
05/25 22:22, , 3F
05/25 22:22, 3F
→
05/25 22:23, , 4F
05/25 22:23, 4F
→
05/25 22:24, , 5F
05/25 22:24, 5F
感謝 附上圖片...
http://i.imgur.com/1jGcT.png

看來可以到此結案了...= =+
※ 編輯: jetzake 來自: 114.24.22.72 (05/25 22:47)
推
05/27 23:29, , 6F
05/27 23:29, 6F
討論串 (同標題文章)