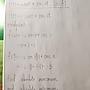[微積] 求極值

看板Math作者 (steve)時間14年前 (2012/03/25 12:18), 編輯推噓0(0推 0噓 14→)
留言14則, 5人參與, 最新討論串7/18 (看更多)
請問一題 x,y,z >= 0 x^2 + y^2 + z^2 = 1 find the maximum of x y z -------- + --------- + -------- 1 + yz 1 + zx 1 + xy 我試過Lagrange multiplier的方法 不過做出來的四個方程式不知道要怎麼解 有什麼比較好的方法嗎 有可以不用為積分的方法嗎 懇請板上高手解答 -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 140.112.24.97
→
03/25 13:08, , 1F
試過梯度嗎
03/25 13:08, 1F
→
03/25 16:48, , 2F
什麼意思..取梯度等於零嗎
03/25 16:48, 2F
→
03/27 23:54, , 3F
由於目標函數及限制式都是變數的對稱形, 猜測其解滿
03/27 23:54, 3F
→
03/27 23:55, , 4F
足 x=y=z. 則 x=y=z=1/√3, 得目標值 3√3/4.
03/27 23:55, 4F
→
03/27 23:57, , 5F
若極大值非如上述, 考慮 x=0, 則目標函數成 y+z,
03/27 23:57, 5F
→
03/27 23:57, , 6F
受限於 y^2+z^2=1. 這很容易得最大值在 x=y=1/√2,
03/27 23:57, 6F
→
03/28 00:01, , 7F
其值 = √2 > 3√3/4. 故最大值可能為 √2, 發生在
03/28 00:01, 7F
→
03/28 00:02, , 8F
x=0,y=z=1/√2, 或 y=0,x=z=1/√2, 或 z=0,x=y=1/√2
03/28 00:02, 8F
→
03/28 00:03, , 9F
又若 x=y=0, 則 z=1, 目標函數值為 z=1.
03/28 00:03, 9F
→
03/28 00:04, , 10F
比較之下, x,y,z一為 0, 另二為1/√2 之結果√2最大.
03/28 00:04, 10F
→
03/28 00:07, , 11F
以上是亂解, Lagrange 方法之方程組解可能不是 x=y=z
03/28 00:07, 11F
→
03/30 08:38, , 12F
03/30 08:38, 12F
→
08/13 16:44, , 13F
其值 = √2 > 3 https://noxiv.com
08/13 16:44, 13F
→
09/17 14:41, , 14F
比較之下, x,y,z https://daxiv.com
09/17 14:41, 14F
‣ 更多 steve1012 的文章
文章代碼(AID): #1FRfoUko (Math)
討論串 (同標題文章)
完整討論串 (本文為第 7 之 18 篇)：
排序： 最新先 | 最舊先 | 留言數
微積
1
2
[微積] 求極值 求極值
attack2000
4年前, 12/31
微積
1
6
[微積] 求極值 求極值
vacuityhu
8年前, 01/30
微積
1
4
[微積] 求極值 求極值
baby800306
8年前, 08/20
微積
0
1
[微積] 求極值 求極值
Ericdion
11年前, 05/28
微積
0
3
[微積] 求極值 求極值
Koguei
12年前, 10/05
在新視窗開啟完整討論串 (共18篇)
‣ 更多 steve1012 的文章
文章代碼(AID): #1FRfoUko (Math)