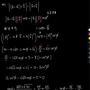看板
[ Math ]
討論串[中學] 高中第4冊向量問題
共 3 篇文章
首頁
上一頁
1
下一頁
尾頁
內容預覽:
|a - 2b| = 2(a - 2b) * b = 2(a * b) - 16. |a - 2b|^2 = 56 - 4(a * b). = (2(a - 2b) * b)^2. = 4[(a * b) - 8]^2. => (a * b)^2 - 15(a * b) + 50 = 0. => a
(還有71個字)
內容預覽:
因為 a-2b 跟 b夾角已知. 而a跟b形成的三角形面積與 a-2b跟b形成的三角形面積相等. 所以只要求出a-2b的長度即可. 令c = a-2b. c - (-2b) = a. c 與 -2b 的夾角為 pi - theta. 利用餘弦定理. |c|^2 + |2b|^2 - 2|c||2b|
(還有253個字)
首頁
上一頁
1
下一頁
尾頁