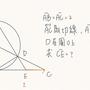
Re: [中學] 國中圓一題求教
※ 引述《ccccc7784 (龍王號)》之銘言:
: 請問這題應該如何解?試過母子相似或是圓冪好像都找不到方向,謝謝各位老師協助
: https://i.imgur.com/Ti7NlgE.jpeg

這題直接三角函數硬上
CE = 2-2tanB
tanB = tan(AOC/2)
(半角公式))
= sin(AOC)/(1+cos(AOC))
= [2/sqrt(5)]/[1+1/sqrt(5)]
= 2/[1+sqrt(5)]
= 2(sqrt(5)-1)/4 = [sqrt(5)-1]/2
CE = 3-sqrt(5)
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 211.23.191.211 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1733200138.A.4AA.html
→
12/03 12:30,
1年前
, 1F
12/03 12:30, 1F
好的,比較複雜但是只用畢氏定理與相似三角形特性:
從D做水平輔助線到AB上交點F
令AE = x
BE = sqrt(4+x^2)
根據相似三角形
考慮三角形ABE系統:
BD = 4/sqrt(4+x^2)
DF = BD*x/sqrt(4+x^2) = 4x/[4+x^2]
考慮三角形ACO系統
DF:AC = OD:OC = 1:sqrt(5)
DF = 2/sqrt(5)
4x*sqrt(5) = 8+2x^2
x^2 - 2*sqrt(5)x+4 = 0
x = sqrt(5) +/-1
因為x<2, 所以x=sqrt(5)-1
所求CE = 2-x = 2-[sqrt(5)-1] = 3-sqrt(5)#
※ 編輯: deathcustom (211.23.191.211 臺灣), 12/03/2024 13:55:04
→
12/03 14:46,
1年前
, 2F
12/03 14:46, 2F
→
12/03 22:21,
1年前
, 3F
12/03 22:21, 3F
討論串 (同標題文章)