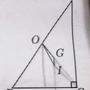
Re: [中學] 直角三角形重心與內心連線

看板Math作者arrenwu (最是清楚哇她咩)時間1年前 (2024/04/01 17:54)推噓2(2推 0噓 4→)

留言6則, 2人參與討論串2/2 (看更多)

※ 引述《yiting428 ()》之銘言： : 大家好 : 如圖 : https://i.imgur.com/6OINrEw.jpg

: 請問如何可以證明 GI 平行 AC？ : 我卡好久了囧 : 目前已嘗試過 Δ=rs=兩股相乘/2 : (r=內切圓半徑，s=周長/2) : 也嘗試過證明r=BC邊/3 : 請大大們賜教了 : 謝謝 : 這問題我感興趣的是：給定三角形 ABC， GI 平行 AC 成立的條件是？用 O 表示原點，a,b,c 分別為 BC, AC, AB 的長度下面寫的 OG, OI 等都是向量: 我們可以用一些已知的幾何結果： OI = a/(a+b+c)*OA + b/(a+b+c)*OB + c/(a+b+c)*OC OG = OA/3 + OB/3 + OC/3 把上面的式子整理一下，可以得到 AI = b/(a+b+c)*AB + c/(a+b+c)*AC AG = AB/3 + AC/3 進一步可以得出 GI = [b/(a+b+c)-1/3]*AB + [c/(a+b+c)-1/3]*AC 給定兩個夾角為θ的向量 X,Y ，定義二維平面的外積 X x Y 為 |X||Y|sinθ GI 與 AC 平行若且惟若 GI x AC = 0 0 = GI x AC = [[b/(a+b+c)-1/3]*AB + [c/(a+b+c)-1/3]*AC] x AC = [b/(a+b+c)-1/3]*(AB x AC) 因為ABC是三角形，AB跟AC不可能平行→ AB x AC ≠ 0 故我們可以得到，GI 與 AC 平行若且惟若 b/(a+b+c) = 1/3 -- 早川秋看到的未來 https://i.imgur.com/aRFJqId.jpg