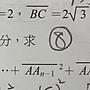Re: [中學] 高中數學兩題已刪文

看板Math作者 (奈何上天造化弄人？)時間4年前 (2021/07/06 16:28), 編輯推噓3(3推 0噓 5→)
留言8則, 3人參與, 4年前最新討論串11/12 (看更多)
※ 引述《bpall (i can do all things)》之銘言： : 請問各位，底下兩題該如何解答， : https://imgur.com/rf45QOZ
: https://imgur.com/ClNPDuv
: 想了老半天，沒什麼想法。 : 麻煩各位大神了！ : 謝謝！！ P_2 = C(2,0)(3/5)^0 * (2/5)^2 + C(2,2)(3/5)^2 * (2/5)^0 = 4/25 + 9/25 = 13/25 P_n = P_(n-1) * 2/5 + [1 - P_(n-1)] * 3/5 = -(1/5)P_(n-1) + 3/5 => P_n = (1/2) - (1/10)(-1/5)^(n-1) => lim P_n = 1/2 n->00 |P_n - 1/2| < 10^(-4) => 5^(n-1) > 10^3 => n > (3/log5) + 1 = 5.2920... => n至少6 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 117.56.175.175 (臺灣) ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1625560108.A.511.html
推
07/06 16:57, 4年前 , 1F
先謝謝大大，但可以請問一下
07/06 16:57, 1F
→
07/06 16:57, 4年前 , 2F
P_n = (1/2) - (1/10)(-1/5)^(n-1) 這麼來的？謝謝
07/06 16:57, 2F
→
07/06 17:08, 4年前 , 3F
P_n = -(1/5)P_(n-1) + 3/5 各項n 乘以(-5)^(n-1)
07/06 17:08, 3F
推
07/06 17:54, 4年前 , 4F
感謝大大！我再好好想一下好了！
07/06 17:54, 4F
推
07/06 18:14, 4年前 , 5F
高中我是這樣學的不知道現在有沒有教:這類的遞迴式
07/06 18:14, 5F
→
07/06 18:14, 4年前 , 6F
可以找α，使得<P_n-α>為等比數列，觀察一下遞迴式
07/06 18:14, 6F
→
07/06 18:14, 4年前 , 7F
不難發現此公比為(-1/5)，將P_n-α=(-1/5)(P_(n-1)-
07/06 18:14, 7F
→
07/06 18:14, 4年前 , 8F
α)與遞迴式比對即可找到α，進而可寫出P_n的通式
07/06 18:14, 8F
‣ 更多 Honor1984 的文章
文章代碼(AID): #1Wv1GiKH (Math)
討論串 (同標題文章)
本文引述了以下文章的的內容：
完整討論串 (本文為第 11 之 12 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共12篇)
‣ 更多 Honor1984 的文章
文章代碼(AID): #1Wv1GiKH (Math)